Number Types and Precision

Python number types

Base python floats and ints

type(123)

int

type(1.23)

float

int(1.23)

1

float(int(1))

1.0

Numpy types preview

Numpy (and many similar libraries) supports many more types

import numpy

numpy.int32(99999)

99999

numpy.int8(99999) # oh no!

-97

numpy.float16(1/3)

0.3333

numpy.float32(1/3)

0.33333334

numpy.float64(1/3)

0.3333333333333333

which one should we use?

Numerical Precision

What is the numerical presision of these displays?

What are the units of the precision? (what word do you naturally give after the precision value?)

What is the maximum total sale and gas volume possible it can read, and what happens if you go over them?

Base-10

Each digit represents a power of 10. The number of digits is the precision needed to display or store the number.

$$ 347 = 3 \times 10^2 + 4 \times 10^1 + 7 \times 10^0 $$

Note $\log_{10}(347) = 2.54...$, which is just under the number of digits (minus a "fractional digit"). $\log_{10}(999) = 2.999..$.

...Decimal Numbers

Use digits to represent negative powers of 10.

$$ 347.625 = 3 \times 10^2 + 4 \times 10^1 + 7 \times 10^0 + 6 \times 10^{-1} + 2 \times 10^{-2} + 5 \times 10^{-3} $$

Floating point numbers ("floats")

E.g., scientific notation.

$$ N_A = 6.022 \times 10^{23}$$$$ h = 6.626 \times 10^{-34}$$

In most languages these can be expressed as 6.626e-34 and 6.022e23

What is the numerical precision?

Floating point means the decimal point can be in a different location for every number, so we need to store that too.

How many digits would be needed to completely store or display the number?

What if we also wanted to include sign for negative numbers?

What would we get if we add them using this representation?

Binary numbers (a.k.a. base-2)

https://mikkegoes.com/computer-science-binary-code-explained/

The basis for all modern computing, though we usually use variations on binary (except for "unsigned integers").

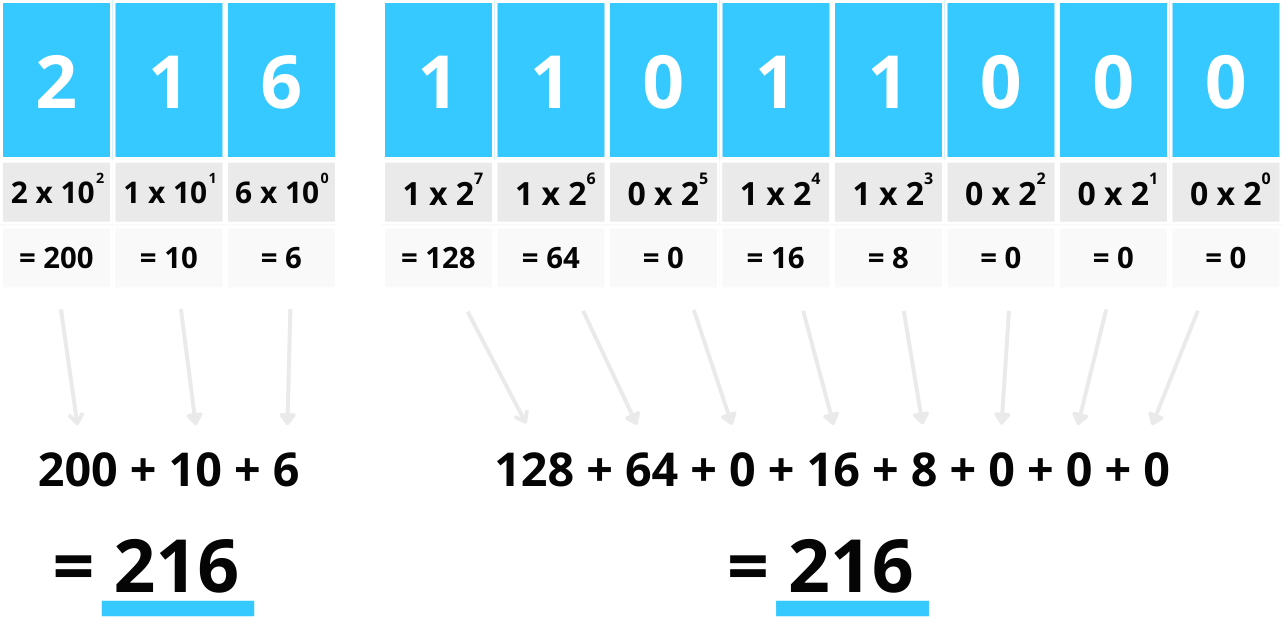
What set of numbers can be represented with the above binary scheme and 8 bits?

bin(216) # gives binary representation of integer

'0b11011000'

import numpy

numpy.base_repr(216, base=2, padding=0)

'11011000'

bits

Note bits is the base-2 precision unit directly analogous to digits in base-10.

216 is 3 digits

11011000 is 8 bits (and also equals 216)

So 3 digits in base-10 is roughly 8 bits in base-2.

What is the largest number possible with 8 bits? with 32 bits? with 64 bits? How many decimal digits do these amount to roughly?

Aside: Information

For a discrete random variable $X$ with possible outcomes $x_i$ that have probabilities $p_i$, the information in an outcome measurement which gives $x_i$ is:

$$ I(x_i) = -\log_2 P(X=x_i) $$

Consider a binary number rpresenting the outcome of a fair coin flip. What is the information in each outcome?

Consider an event which is 8 independent coin flips of a fair coin resulting in, e.g., 10110101. What is the infomation value?

Aside: Hexadecimal

Base-16 system. Effectively groups four binary digits into each hex digit.

for k in range(0,32):
    print(f'{k:4d}  {bin(k):>8s} {hex(k):>5s}.')

   0       0b0   0x0.
   1       0b1   0x1.
   2      0b10   0x2.
   3      0b11   0x3.
   4     0b100   0x4.
   5     0b101   0x5.
   6     0b110   0x6.
   7     0b111   0x7.
   8    0b1000   0x8.
   9    0b1001   0x9.
  10    0b1010   0xa.
  11    0b1011   0xb.
  12    0b1100   0xc.
  13    0b1101   0xd.
  14    0b1110   0xe.
  15    0b1111   0xf.
  16   0b10000  0x10.
  17   0b10001  0x11.
  18   0b10010  0x12.
  19   0b10011  0x13.
  20   0b10100  0x14.
  21   0b10101  0x15.
  22   0b10110  0x16.
  23   0b10111  0x17.
  24   0b11000  0x18.
  25   0b11001  0x19.
  26   0b11010  0x1a.
  27   0b11011  0x1b.
  28   0b11100  0x1c.
  29   0b11101  0x1d.
  30   0b11110  0x1e.
  31   0b11111  0x1f.

Floating point number representation

We must represent the sign, the decimal part, and the exponent all in our 32 or 64 bits of space. So we use some subset of bits to represent each part:

$$x \sim (-1)^{\text{sign}} \times \text{fraction} \times 2^\text{exponent}\$$

IEEE 754 standard for representing a real number. 32 and 64 bit cases </br></br>

Note the fractional part means the binary fraction. Save space by not representing leading 1 in e.g., 1.101011...

Extras

Some extra info besides numbers.

• two version of zero are possible, +0 and -0, depending on sign bit
• $\pm$ Infinity = exponents all 1's, fraction all 0's
• Not-a-number (NaN) = exponents all 1's, fraction not all 0's.
• Subnormal numbers - used to extend the range of small numbers a bit further

https://learn.microsoft.com/en-us/cpp/build/ieee-floating-point-representation?view=msvc-170

-1.0*0.0

-0.0

1.0/0.0

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
~\AppData\Local\Temp\ipykernel_26264\832528835.py in <module>
----> 1 1./0.

ZeroDivisionError: float division by zero

0.0/0.0

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
~\AppData\Local\Temp\ipykernel_26264\1949058463.py in <module>
----> 1 0.0/0.0

ZeroDivisionError: float division by zero

Python math library

import math # load python math library
math.inf * 3

inf

math.inf/math.inf

nan

Numpy inf and nan

import numpy

-1.0*numpy.float32(0.0)

-0.0

import numpy

-1./numpy.float32(0.)

C:\Users\micro\AppData\Local\Temp\ipykernel_29412\4148764609.py:3: RuntimeWarning: divide by zero encountered in true_divide
  -1./numpy.float32(0.)

-inf

0.0/numpy.float32(0.0)

C:\Users\micro\AppData\Local\Temp\ipykernel_29412\3555820988.py:1: RuntimeWarning: invalid value encountered in true_divide
  0.0/numpy.float32(0.0)

nan

0*numpy.nan

nan

numpy.inf*numpy.nan

nan

Checking for nan and inf directly

numpy.inf == 1/numpy.float32(0.0)

C:\Users\micro\AppData\Local\Temp\ipykernel_29412\2350908150.py:1: RuntimeWarning: divide by zero encountered in true_divide
  numpy.inf == 1/numpy.float32(0.0)

True

numpy.nan == numpy.nan # !!

False

numpy.isnan(numpy.float32(0)/numpy.float32(0))

C:\Users\micro\AppData\Local\Temp\ipykernel_29412\4269917502.py:1: RuntimeWarning: invalid value encountered in float_scalars
  numpy.isnan(numpy.float32(0)/numpy.float32(0))

True

numpy.isinf(1.0/numpy.float32(0))

C:\Users\micro\AppData\Local\Temp\ipykernel_29412\468334143.py:1: RuntimeWarning: divide by zero encountered in true_divide
  numpy.isinf(1.0/numpy.float32(0))

True

Commonly used number types

Various combinations of short vs long (or single versus double) int versus float, signed versus unsigned (for ints).

Details depends on platform (Linux vs Windows vs Max) and has evolved over time.

Common names	bits	Python name	Numpy name(s)
boolean (bool)	8		numpy.bool
character (char)	8		numpy.char
integers (int)	32	int	numpy.intc, numpy.int32
unsigned integers (uint)	32		numpy.uint32
floating-pointing numbers (float, single)	32,64	float	numpy.float32, numpy.float64
double precision floating point numbers (double)	64		numpy.double
short integers (short)	16		numpy.short
long integers (long)	32,64		numpy.long
double long integers (longlong)	64,128?		numpy.longlong
unsigned long integers (ulong)	32,64		numpy.ulong

Precision (a.k.a. number of bits) is often added to the type name, e.g. float32.

https://en.cppreference.com/w/cpp/language/types </br> https://numpy.org/devdocs/user/basics.types.html

Windows

https://learn.microsoft.com/en-us/cpp/cpp/fundamental-types-cpp?view=msvc-170

Bits of precision versus digits

Number of decimal digits from the number of binary exponent bits

• 32 bit floats have about 7 digits of precision
• 64 bit floats have about 16 digits precision

Must keep in mind that decimal numbers are always approximate.

https://docs.python.org/3/tutorial/floatingpoint.html

Do these precision digits make sense within the IEEE standard? (recall 23 bits fraction for 32-bit float)

Multiplying a matrix by its inverse using numpy

A = numpy.random.randint(0, 10, size=(3, 3))
A_inv = numpy.linalg.inv(A)
print(A,'\n')
print(A_inv,'\n')
print(A@A_inv) # matrix times its inverse should be identity

[[3 1 6]
 [7 3 0]
 [1 4 8]] 

[[ 0.14457831  0.09638554 -0.10843373]
 [-0.3373494   0.10843373  0.25301205]
 [ 0.15060241 -0.06626506  0.01204819]] 

[[1.00000000e+00 5.55111512e-17 2.77555756e-17]
 [5.55111512e-17 1.00000000e+00 5.55111512e-17]
 [0.00000000e+00 0.00000000e+00 1.00000000e+00]]

Baseline assumption: Floating point computations are not exact

$$ a+b \approx c$$

Result will be nearest floating point number that can be represented with the binary system used.

(There are libraries which support exact arithmetic. A niche area.)

1 + 1e-12

1.000000000001

1 + 1e-25

1.0

1e-25

1e-25

Logic still expects exactness

1 + 1e-25 == 1

True

1 + 1e-12 == 1

False

1e-25 + 1e-12

1.0000000000001e-12

0.1 + 0.1 + 0.1 == 0.3

False

0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 == 1.0

False

# sometimes it can come out exact

a=3.0
b=a/3.0
c=b*3.0
c==a

True

Doing inexact logic

Basically check that the numbers only differ by an amount based on the precision (e.g. $10^{-7}$ for floats).

import math

math.isclose(0.1 + 0.1 + 0.1, 0.3)

True

round(0.1 + 0.1 + 0.1, 5) == round(0.3, 5) # round to 5 digits precision

True

round(0.1234567,5)

0.12346

"hard zeros"

special case when "0.0" is exactly zero in our representation (e.g., binary 00000000)

0.1 + 0.1 + 0.1 - 0.3 == 1.0 

False

1.0 - 1.0 == 0.0 

True

Overflow and Underflow

Overflow = not enough bits to represent number (number too big, positive or negative)

Underflow = not enough precision to represent number (number too small)

# Integer Overflow (int8)

import numpy

a = numpy.int8(120)
b = numpy.int8(10)
a + b

C:\Users\micro\AppData\Local\Temp\ipykernel_29412\722240833.py:7: RuntimeWarning: overflow encountered in byte_scalars
  a + b

-126

Why does this happen when $2^8 = 256$?

# Integer Overflow (int16) 

a16 = numpy.int16(32760)
b16 = numpy.int16(10)
a16 + b16

C:\Users\micro\AppData\Local\Temp\ipykernel_29412\1581886380.py:5: RuntimeWarning: overflow encountered in short_scalars
  a16 + b16

-32766

2**16

65536

numpy.iinfo(numpy.int16)

iinfo(min=-32768, max=32767, dtype=int16)

32768+32767+1 # all numbers used - (no negative zero due to use of "2s complement" format)

65536

note no negative zero in ints, just floats

-1.0*0.0

-0.0

-1*0

0

It's just one extra number, so can ignore when considering precision generally

# Negative Integer "Overflow" (int8)

x = numpy.int8(-120)
y = numpy.int8(-10)
x + y

C:\Users\micro\AppData\Local\Temp\ipykernel_29412\1500945009.py:5: RuntimeWarning: overflow encountered in byte_scalars
  x + y

126

numpy.int8(-130)

126

# Floating-Point Overflow 

import numpy

a = numpy.float32(1e38)
b = numpy.float32(10)
a * b

C:\Users\micro\AppData\Local\Temp\ipykernel_29412\517216590.py:7: RuntimeWarning: overflow encountered in float_scalars
  a * b

inf

# Floating-Point Underflow 

x = numpy.float32(1e-38)
y = numpy.float32(1e-10)
x * y

0.0

x * y == 0.0

True

Note no warning since we should be expecting finite precision already and should have planned to deal with it. Whereas overflow causes much bigger errors so we are given warning (can detect this in a program).

# Float64 overflow

a64 = numpy.float64(1e308)
b64 = numpy.float64(10)
a64 * b64

C:\Users\micro\AppData\Local\Temp\ipykernel_29412\3767394089.py:5: RuntimeWarning: overflow encountered in double_scalars
  a64 * b64

inf

# float64 underflow

x64 = numpy.float64(1e-308)
y64 = numpy.float64(1e-16)
x64 * y64

0.0

Preventing Overflow

Use larger number for result "type promotion"

import numpy

a = numpy.int8(120)
b = numpy.int8(10)

a + b

C:\Users\micro\AppData\Local\Temp\ipykernel_29412\1681399786.py:6: RuntimeWarning: overflow encountered in byte_scalars
  a + b

-126

# Promote to int16 before addition
numpy.int16(a) + numpy.int16(b)

130

Aside: Getting representation details

# function to get underlying precision of compute (e.g., 64-bit CPU)

import numpy

numpy.distutils.system_info.platform_bits

64

# just calculates number of bits in an int for us

x = 31

x.bit_length()

5

numpy finfo function

x=numpy.float64(1.0)
np.finfo(x)

finfo(resolution=1e-15, min=-1.7976931348623157e+308, max=1.7976931348623157e+308, dtype=float64)

numpy.finfo(numpy.float32)

finfo(resolution=1e-06, min=-3.4028235e+38, max=3.4028235e+38, dtype=float32)

numpy.finfo(float)

finfo(resolution=1e-15, min=-1.7976931348623157e+308, max=1.7976931348623157e+308, dtype=float64)

In python an int is actually a class, not just a number in a memory location

import sys
myint = 12
sys.getsizeof(myint) # class size in sumber of bytes

28

Recap

• Numbers in Python can be either int or float
• These are represented on your computer by binary numbers, usually with 64 bits
• A few other special symbols such as inf, and nan (and negative zero) are included in the float standard, and math libraries use them, e.g. 1/0 -> inf
• The limited number of bits in these representations limit the range of numbers and precision possible
• As a result, mathematical values and operations are usually approximate, truncated based on maximum precision possible
• Underflow occurs when a number is too small and you get a zero instead.
• Overflow occurs when a number is too large and you get an error/warning along with a very wrong number (e.g., wraparound).
• you need to be aware of these dangers and errors and control or account for them