Unstructured Data & Natural Language Processing

Topic 2: Text & Sequence Processing
This topic:¶
- Character encodings
- Regular expressions
- Tokenization, segmentation, & stemming
- Approximate sequence matching
Reading:
- https://www.oreilly.com/library/view/fluent-python/9781491946237/ch04.html
- J&M Chapter 2, "Regular Expressions, Text Normalization, and Edit Distance"
- "The Algorithm Design Manual, 3e," Chapter 8, Steven Skiena, 2020.
- OSU Molecular Biology Primer, Chapter 21: https://open.oregonstate.education/computationalbiology/chapter/bioinformatics-knick-knacks-and-regular-expressions/
Motivation¶
Processing formatted records which are in varying text formats, such as converting different date formats '01/01/24' vs 'Jan 1, 2024' vs '1 January 2024' to a single numerical variable
Processing survey data or health records in text format, use NLP to convert unstructured text to a categorical variable.
Processing other sequential data such as DNA or biological signals
Modern A.I. (Large Language Models) are trained to solve NLP problems using large collections of text. Model incorporates general knowlege for any topic broadly understood, such as science, health, psychology, and can be applied outside of NLP problems
Text Processing Levels¶
- Character
- Words
- Sentences / multiple words
- Paragraphs / multiple sentences
- Document
- Corpus / multiple documents
Source: Taming Text, p 9
Character¶
- Character encodings
- Case (upper and lower)
- Punctuation
- Numbers
Indicate by quotes (either single or double works)
x = 'a'
y = '3'
z = '&'
print(x,y,z)
a 3 &
Words¶
- Word segmentation: dividing text into words. Fairly easy for English and other languages that use whitespace; much harder for languages like Chinese and Japanese.
- Stemming: the process of shortening a word to its base or root form.
- Abbreviations, acronyms, and spelling. All help understand words.
In Python we store words into strings ~ sequences of characters. Will do this soon.
Sentences¶
- Sentence boundary detection: a well-understood problem in English, but is still not perfect.
- Phrase detection: San Francisco and quick red fox are examples of phrases.
- Parsing: breaking sentences down into subject-verb and other relation- ships often yields useful information about words and their relation- ships to each other.
- Combining the definitions of words and their relationships to each other to determine the meaning of a sentence.
Paragraphs¶
At this level, processing becomes more difficult in an effort to find deeper understanding of an author’s intent.
For example, algorithms for summarization often require being able to identify which sentences are more important than others.
Document¶
Similar to the paragraph level, understanding the meaning of a document often requires knowledge that goes beyond what’s contained in the actual document.
Authors often expect readers to have a certain background or possess certain reading skills.
Corpus¶
At this level, people want to quickly find items of interest as well as group related documents and read summaries of those documents.
Applications that can aggregate and organize facts and opinions and find relationships are particularly useful.
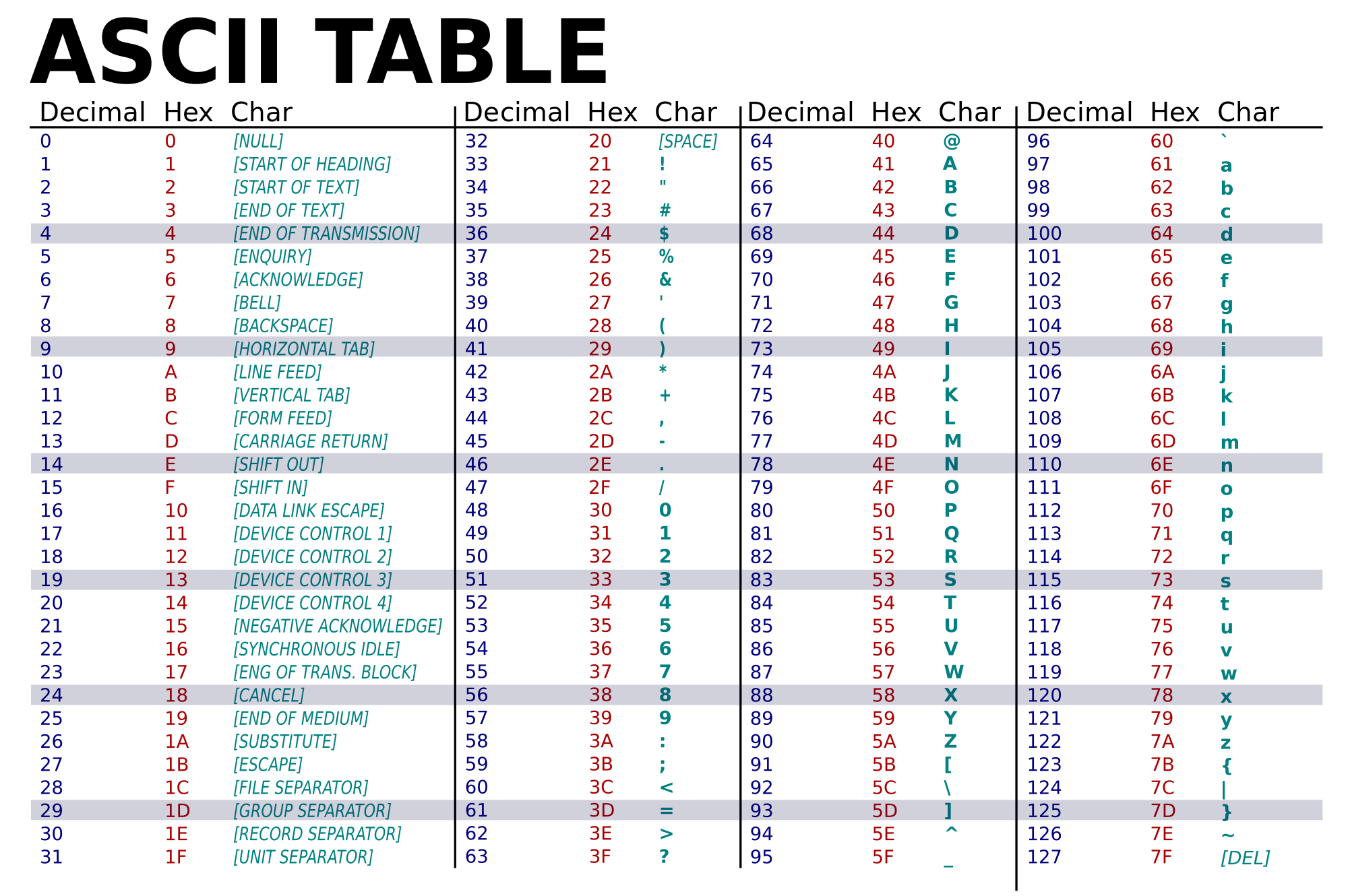
I. Character Encodings¶
Character Encodings - map character to binary¶
- ASCII - 7 bits
- char - 8-bit - a-z,A-Z,0-9,...
- multi-byte encodings for other languages
ascii(38)
'38'
str(38)
'38'
chr(38)
'&'
Unicode¶
Unicode - "code points"¶
lookup table of unique numbers denoting every possible character
Encoding still needed -- various standards
- UTF-8 (dominant standard),16 - variable-length
- UTF-32 - 4-byte
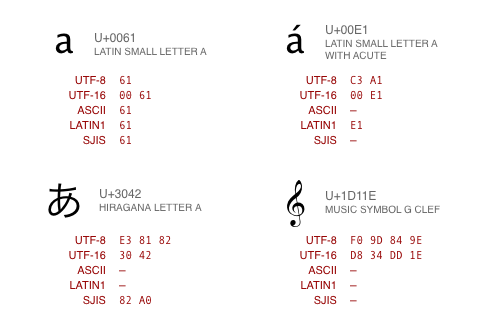
chr(2^30+1) # for python 3
'\x1d'
Mojibake¶

Incorrect, unreadable characters shown when computer software fails to show text correctly.
It is a result of text being decoded using an unintended character encoding.
Very common in Japanese websites, hence the name:
文字 (moji) "character" + 化け (bake) "transform"
II. String Processing and Regular Expressions¶
Background: Lists [item1, item2, item3]¶
- Sequence of values - order & repeats ok
- Mutable
- Concatenate lists with "+"
- Index with mylist[index] - note zero based
L = [1,2,3,4,5,6]
print(L)
print("length =",len(L))
print(L[0],L[1],L[2])
[1, 2, 3, 4, 5, 6] length = 6 1 2 3
[1,2,3,4,5][3]
4
Slices - mylist[start:end:step]¶
Matlabesque way to select sub-sequences from list
- If first index is zero, can omit - mylist[:end:step]
- If last index is length-1, can omit - mylist[::step]
- If step is 1, can omit mylist[start:end]
Make slices for even and odd indexed members of this list.
[1,2,3,4,5][:3]
[1, 2, 3]
Strings¶
List of characters
s = 'Hello there'
print(s)
Hello there
print(s[0],s[2])
H l
print(s[:2])
He
x = 'hello'
y = 'there'
z = '!'
print(x,y,z) # x,y,z is actually a tuple
hello there !
# addition concatenates lists or characters or strings
xyz = x+y+z
print(xyz)
hellothere!
How do we fix the spacing in this sentence?
Other useful operations¶
xyz = 'hello there'
print(xyz.split(' '))
['hello', 'there']
print(xyz.split())
['hello', 'there']
print(xyz.split('e'))
['h', 'llo th', 'r', '']
mylist = xyz.split()
print(mylist)
['hello', 'there']
print(' '.join(mylist))
hello there
print('_'.join(mylist))
hello_there
from string import *
whos
Variable Type Data/Info
---------------------------------------
Formatter type <class 'string.Formatter'>
L list n=6
Template type <class 'string.Template'>
ascii_letters str abcdefghijklmnopqrstuvwxy<...>BCDEFGHIJKLMNOPQRSTUVWXYZ
ascii_lowercase str abcdefghijklmnopqrstuvwxyz
ascii_uppercase str ABCDEFGHIJKLMNOPQRSTUVWXYZ
capwords function <function capwords at 0x00000181E7B2DF80>
dat0 list n=3
dat1 list n=4
digits str 0123456789
hexdigits str 0123456789abcdefABCDEF
literal1 str calendar
literal2 str calandar
literal3 str celender
mylist list n=2
octdigits str 01234567
pattern2 str c[ae]l[ae]nd[ae]r
patterns str calendar|calandar|celender
printable str 0123456789abcdefghijklmno<...>/:;<=>?@[\]^_`{|}~ \n
punctuation str !"#$%&'()*+,-./:;<=>?@[\]^_`{|}~
re module <module 're' from 'C:\\Us<...>4\\Lib\\re\\__init__.py'>
s str Hello there
st str calendar foo calandar cal celender calli
string module <module 'string' from 'C:<...>_083124\\Lib\\string.py'>
sub_pattern str [ae]
whitespace str \n
x str hello
xyz str hello there
xyz2 str hellothere2!
y str there
z str !
Student Activity¶
Let's make a simple password generator function!
Your code should return something like this:
'kZmuSUVeVC'
'mGEsuIfl91'
'FEFsWwAgLM'
import random
import string
n = 10
pw = ''.join((random.choice(string.ascii_letters + string.digits) for n in range(n)))
Regular Expressions ("regex")¶
Used in grep, awk, ed, perl, ...
Regular expression is a pattern matching language, the "RE language".
A Domain Specific Language (DSL). Powerful (but limited language). E.g. SQL, Markdown.

from re import *
whos
Variable Type Data/Info
----------------------------------------
A RegexFlag re.ASCII
ASCII RegexFlag re.ASCII
DOTALL RegexFlag re.DOTALL
Formatter type <class 'string.Formatter'>
I RegexFlag re.IGNORECASE
IGNORECASE RegexFlag re.IGNORECASE
L RegexFlag re.LOCALE
LOCALE RegexFlag re.LOCALE
M RegexFlag re.MULTILINE
MULTILINE RegexFlag re.MULTILINE
Match type <class 're.Match'>
NOFLAG RegexFlag re.NOFLAG
Pattern type <class 're.Pattern'>
RegexFlag EnumType <flag 'RegexFlag'>
S RegexFlag re.DOTALL
Template type <class 'string.Template'>
U RegexFlag re.UNICODE
UNICODE RegexFlag re.UNICODE
VERBOSE RegexFlag re.VERBOSE
X RegexFlag re.VERBOSE
ascii_letters str abcdefghijklmnopqrstuvwxy<...>BCDEFGHIJKLMNOPQRSTUVWXYZ
ascii_lowercase str abcdefghijklmnopqrstuvwxyz
ascii_uppercase str ABCDEFGHIJKLMNOPQRSTUVWXYZ
capwords function <function capwords at 0x00000181E7B2DF80>
chars str abcdefghijklmnopqrstuvwxy<...>LMNOPQRSTUVWXYZ0123456789
compile function <function compile at 0x00000181E76CDB20>
dat0 list n=3
dat1 list n=4
digits str 0123456789
error type <class 're.error'>
escape function <function escape at 0x00000181E76CDD00>
findall function <function findall at 0x00000181E76CD9E0>
finditer function <function finditer at 0x00000181E76CDA80>
fullmatch function <function fullmatch at 0x00000181E76CD580>
hexdigits str 0123456789abcdefABCDEF
k int 9
literal1 str calendar
literal2 str calandar
literal3 str celender
match function <function match at 0x00000181E7634400>
mylist list n=2
n int 10
newchar str I
octdigits str 01234567
pattern2 str c[ae]l[ae]nd[ae]r
patterns str calendar|calandar|celender
printable str 0123456789abcdefghijklmno<...>/:;<=>?@[\]^_`{|}~ \n
punctuation str !"#$%&'()*+,-./:;<=>?@[\]^_`{|}~
purge function <function purge at 0x00000181E76CDBC0>
pw str Yi7RZhEMvI
r float 0.5457937230425709
random module <module 'random' from 'C:<...>_083124\\Lib\\random.py'>
re module <module 're' from 'C:\\Us<...>4\\Lib\\re\\__init__.py'>
s str Hello there
search function <function search at 0x00000181E76CD760>
split function <function split at 0x00000181E76CD940>
st str calendar foo calandar cal celender calli
string module <module 'string' from 'C:<...>_083124\\Lib\\string.py'>
sub function <function sub at 0x00000181E76CD800>
sub_pattern str [ae]
subn function <function subn at 0x00000181E76CD8A0>
template function <function template at 0x00000181E76CDC60>
whitespace str \n
x str hello
xyz str hello there
xyz2 str hellothere2!
y str there
z str !
Motivating example¶
Write a regex to match common misspellings of calendar: "calendar", "calandar", or "celender"
# Let's explore how to do this
# Patterns to match
dat0 = ["calendar", "calandar", "celender"]
# Patterns to not match
dat1 = ["foo", "cal", "calli", "calaaaandar"]
# Interleave them
st = " ".join([item for pair in zip(dat0, dat1) for item in pair])
st
'calendar foo calandar cal celender calli'
# You match it with literals
literal1 = 'calendar'
literal2 = 'calandar'
literal3 = 'celender'
patterns = "|".join([literal1, literal2, literal3])
patterns
'calendar|calandar|celender'
import re
print(re.findall(patterns, st))
['calendar', 'calandar', 'celender']
... a better way¶
Let's write it with regex language
sub_pattern = '[ae]'
pattern2 = sub_pattern.join(["c","l","nd","r"])
print(pattern2)
c[ae]l[ae]nd[ae]r
print(st)
re.findall(pattern2, st)
calendar foo calandar cal celender calli
['calendar', 'calandar', 'celender']
Regex Terms¶
- target string: This term describes the string that we will be searching, that is, the string in which we want to find our match or search pattern.
- search expression: The pattern we use to find what we want. Most commonly called the regular expression.
- literal: A literal is any character we use in a search or matching expression, for example, to find ind in windows the ind is a literal string - each character plays a part in the search, it is literally the string we want to find.
- metacharacter: A metacharacter is one or more special characters that have a unique meaning and are NOT used as literals in the search expression. For example "." means any character.
- escape sequence: An escape sequence is a way of indicating that we want to use one of our metacharacters as a literal.
function(search_expression, target_string)¶
pick function based on goal (find all matches, replace matches, find first match, ...)
form search expression to account for variations in target we allow. E.g. possible misspellings.
- findall() - Returns a list containing all matches
- search() - Returns a Match object if there is a match anywhere in the string
- split() - Returns a list where the string has been split at each match
- sub() - Replaces one or many matches with a string
- match() apply the pattern at the start of the string
Metacharacters¶
special characters that have a unique meaning
[] A set of characters. Ex: "[a-m]"
\ Signals a special sequence, also used to escape special characters). Ex: "\d"
. Any character (except newline character). Ex: "he..o"
^ Starts with. Ex: "^hello"
$ Ends with. Ex: "world$"
* Zero or more occurrences. Ex: "aix*"
+ One or more occurrences. Ex: "aix+"
{} Specified number of occurrences. Ex: "al{2}"
| Either or. Ex: "falls|stays"
() Capture and groupEscape sequence "\"¶
A way of indicating that we want to use one of our metacharacters as a literal.
In a regular expression an escape sequence is metacharacter \ (backslash) in front of the metacharacter that we want to use as a literal.
Ex: If we want to find \file in the target string c:\file then we would need to use the search expression \\file (each \ we want to search for as a literal (there are 2) is preceded by an escape sequence ).
Special Escape Sequences¶
- \A - specified characters at beginning of string. Ex: "\AThe"
- \b - specified characters at beginning or end of a word. Ex: r"\bain" r"ain\b"
- \B - specified characters present but NOT at beginning (or end) of word. Ex: r"\Bain" r"ain\B"
- \d - string contains digits (numbers from 0-9)
- \D - string DOES NOT contain digits
- \s - string contains a white space character
- \S - string DOES NOT contain a white space character
- \w - string contains any word characters (characters from a to Z, digits from 0-9, and the underscore _ character)
- \W - string DOES NOT contain any word characters
- \Z - specified characters are at the end of the string
Set¶
a set of characters inside a pair of square brackets [] with a special meaning:
- [arn] one of the specified characters (a, r, or n) are present
- [a-n] any lower case character, alphabetically between a and n
- [^arn] any character EXCEPT a, r, and n
- [0123] any of the specified digits (0, 1, 2, or 3) are present
- [0-9] any digit between 0 and 9
- [0-5][0-9] any two-digit numbers from 00 and 59
- [a-zA-Z] any character alphabetically between a and z, lower case OR upper case
- [+] In sets, +, *, ., |, (), $,{} has no special meaning, so [+] means any + character in the string
Ex: Matching phone numbers¶
target_string = 'fgsfdgsgf 415-805-1888 xxxddd 800-555-1234'
pattern1 = '[0-9][0-9][0-9]-[0-9][0-9][0-9]-[0-9][0-9][0-9][0-9]'
print(re.findall(pattern1,target_string))
['415-805-1888', '800-555-1234']
pattern2 = '\\d\\d\\d-\\d\\d\\d-\\d\\d\\d\\d'
print(re.findall(pattern2,target_string))
['415-805-1888', '800-555-1234']
pattern3 = '\\d{3}-\\d{3}-\\d{4}'
print(re.findall(pattern3,target_string))
['415-805-1888', '800-555-1234']
\d{3}-\d{3}-\d{4} uses Quantifiers.
Quantifiers: allow you to specify how many times the preceding expression should match.
{} is extact quantifier.
print(re.findall('x?','xxxy'))
['x', 'x', 'x', '', '']
print(re.findall('x+','xxxy'))
['xxx']
Capturing groups¶
Problem: You have odd line breaks in your text.
text = 'Long-\nterm problems with short-\nterm solutions.'
print(text)
Long- term problems with short- term solutions.
text.replace('-\n','\n')
'Long\nterm problems with short\nterm solutions.'
Solution: Write a regex to find the "dash with line break" and replace it with just a line break.
import re
# 1st Attempt
text = 'Long-\nterm problems with short-\nterm solutions.'
re.sub('(\\w+)-\\n(\\w+)', r'-', text)
'- problems with - solutions.'
Not right. We need capturing groups.
Capturing groups allow you to apply regex operators to the groups that have been matched by regex.
For for example, if you wanted to list all the image files in a folder. You could then use a pattern such as ^(IMG\d+\.png)$ to capture and extract the full filename, but if you only wanted to capture the filename without the extension, you could use the pattern ^(IMG\d+)\.png$ which only captures the part before the period.
re.sub(r'(\w+)-\n(\w+)', r'\1-\2', text)
'Long-term problems with short-term solutions.'
The parentheses around the word characters (specified by \w) means that any matching text should be captured into a group.
The '\1' and '\2' specifiers refer to the text in the first and second captured groups.
"Long" and "term" are the first and second captured groups for the first match.
"short" and "term" are the first and second captured groups for the next match.
NOTE: 1-based indexing
III. Tokenization, segmentation, & stemming¶
Sentence segmentation:¶
Dividing a stream of language into component sentences.
Sentences can be defined as a set of words that is complete in itself, typically containing a subject and predicate.
Sentence segmentation typically done using punctuation, particularly the full stop character "." as a reasonable approximation.
Complications because punctuation also used in abbreviations, which may or may not also terminate a sentence.
For example, Dr. Evil.
Example¶
A Confederacy Of Dunces
By John Kennedy Toole
A green hunting cap squeezed the top of the fleshy balloon of a head. The green earflaps, full of large ears and uncut hair and the fine bristles that grew in the ears themselves, stuck out on either side like turn signals indicating two directions at once. Full, pursed lips protruded beneath the bushy black moustache and, at their corners, sank into little folds filled with disapproval and potato chip crumbs. In the shadow under the green visor of the cap Ignatius J. Reilly’s supercilious blue and yellow eyes looked down upon the other people waiting under the clock at the D.H. Holmes department store, studying the crowd of people for signs of bad taste in dress.
sentence_1 = A green hunting cap squeezed the top of the fleshy balloon of a head.
sentence_2 = The green earflaps, full of large ears and uncut hair and the fine bristles that grew in the ears themselves, stuck out on either side like turn signals indicating two directions at once.
sentence_3 = Full, pursed lips protruded beneath the bushy black moustache and, at their corners, sank into little folds filled with disapproval and potato chip crumbs.
sentence_4 = In the shadow under the green visor of the cap Ignatius J. Reilly’s supercilious blue and yellow eyes looked down upon the other people waiting under the clock at the D.H. Holmes department store, studying the crowd of people for signs of bad taste in dress.
Code version 1¶
text = """A green hunting cap squeezed the top of the fleshy balloon of a head. The green earflaps, full of large ears and uncut hair and the fine bristles that grew in the ears themselves, stuck out on either side like turn signals indicating two directions at once. Full, pursed lips protruded beneath the bushy black moustache and, at their corners, sank into little folds filled with disapproval and potato chip crumbs. In the shadow under the green visor of the cap Ignatius J. Reilly’s supercilious blue and yellow eyes looked down upon the other people waiting under the clock at the D.H. Holmes department store, studying the crowd of people for signs of bad taste in dress. """
import re
pattern = "|".join(['!', # end with "!"
'\\?', # end with "?"
'\\.\\D', # end with "." and the full stop is not followed by a number
'\\.\\s']) # end with "." and the full stop is followed by a whitespace
print(pattern)
!|\?|\.\D|\.\s
re.split(pattern, text)
['A green hunting cap squeezed the top of the fleshy balloon of a head', 'The green earflaps, full of large ears and uncut hair and the fine bristles that grew in the ears themselves, stuck out on either side like turn signals indicating two directions at once', 'Full, pursed lips protruded beneath the bushy black moustache and, at their corners, sank into little folds filled with disapproval and potato chip crumbs', 'In the shadow under the green visor of the cap Ignatius J', 'Reilly’s supercilious blue and yellow eyes looked down upon the other people waiting under the clock at the D', '', 'Holmes department store, studying the crowd of people for signs of bad taste in dress', '']
pattern = r"(?<!\w\.\w.)(?<![A-Z][a-z]\.)(?<=\.|\?)\s"
re.split(pattern, text)
['A green hunting cap squeezed the top of the fleshy balloon of a head.', 'The green earflaps, full of large ears and uncut hair and the fine bristles that grew in the ears themselves, stuck out on either side like turn signals indicating two directions at once.', 'Full, pursed lips protruded beneath the bushy black moustache and, at their corners, sank into little folds filled with disapproval and potato chip crumbs.', 'In the shadow under the green visor of the cap Ignatius J.', 'Reilly’s supercilious blue and yellow eyes looked down upon the other people waiting under the clock at the D.H. Holmes department store, studying the crowd of people for signs of bad taste in dress.', '']
Code by using a library¶
...next class
Tokenization¶
Breaking a stream of text up into words, phrases, symbols, or other meaningful elements called tokens
The simplest way to tokenize is to split on white space
sentence1 = 'Sky is blue and trees are green'
sentence1.split(' ')
['Sky', 'is', 'blue', 'and', 'trees', 'are', 'green']
sentence1.split() # in fact it's the default
['Sky', 'is', 'blue', 'and', 'trees', 'are', 'green']
Sometimes you might also want to deal with abbreviations, hypenations, puntuations and other characters.
In those cases, you would want to use regex.
However, going through a sentence multiple times can be slow to run if the corpus is long
import re
sentence2 = 'This state-of-the-art technology is cool, isn\'t it?'
sentence2 = re.sub('-', ' ', sentence2)
sentence2 = re.sub('[,|.|?]', '', sentence2)
sentence2 = re.sub('n\'t', ' not', sentence2)
print(sentence2)
sentence2_tokens = re.split('\\s+', sentence2)
print(sentence2_tokens)
This state of the art technology is cool is not it ['This', 'state', 'of', 'the', 'art', 'technology', 'is', 'cool', 'is', 'not', 'it']
In this case, there are 11 tokens and the size of the vocabulary is 10
print('Number of tokens:', len(sentence2_tokens))
print('Number of vocabulary:', len(set(sentence2_tokens)))
Number of tokens: 11 Number of vocabulary: 10
Tokenization is a major component of modern language models and A.I., where tokens are defined more generally.
Morphemes¶
A morpheme is the smallest unit of language that has meaning. Two types:
- stems
- affixes (suffixes, prefixes, infixes, and circumfixes)
Example: "unbelievable"
What is the stem? What is the affixes?
"believe" is a stem.
"un" and "able" are affixes.
What we usually want to do in NLP preprocessing is get the stem a stem by eliminating the affixes from a token.
Stemming¶
Stemming usually refers to a crude heuristic process that chops off the ends of words.
Ex: automates, automating and automatic could be stemmed to automat
Exercise: how would you implement this using regex? What difficulties would you run into?
Lemmatization¶
Lemmatization aims to remove inflectional endings only and to return the base or dictionary form of a word, which is known as the lemma.
This is doing things properly with the use of a vocabulary and morphological analysis of words.
How are stemming and lemmatization similar/different?
Summary¶
- Tokenization separates words in a sentence
- You would normalize or process the sentence during tokenization to obtain sensible tokens
- These normalizations include:
- Replacing special characters with spaces such as
,.-=!using regex - Lowercasing
- Stemming to remove the suffix of tokens to make tokens more uniform
- Replacing special characters with spaces such as
- There are three types of commonly used stemmers. They are Porter, Snowball and Lancaster
- Lancaster is the fastest and most aggressive, Snowball is a balance between speed and quality
Bioinformatics¶
Many analogous tasks in processing DNA and RNA sequences
- Finding exact matches for shorter sequence within long sequence
- Inexact or approximate matching?
IV. Approximate Sequence Matching¶
Exact Matching¶
Fing places where pattern $P$ is found within text $T$.
What python functions do this?
Also very important problem. Not trivial for massive datasets.
Alignment - compare $P$ to same-length substring of $T$ at some starting point.

How many calculations will this take in the most naive approach possible?
Improving on the Naive Exact-matching algorithm¶
Naive approach: test all possible alignments for match.
Ideas for improvement:
- stop comparing given alignment at first mismatch.
- use result of prior alignments to shorten or skip subsequent alignments.
Approximate matching: Motivational problems¶
- Matching Regular Expressions to text efficiently
- Biological sequence alignment between different species
- Matching noisy trajectories through space
- Clustering sequences into a few groups of most similar classes
- Applying k Nearest Neighbors classification to sequences
Pre-filtering, Pruning, etc.¶
When performing a slow search algorithm over a large dataset, start with fast algorithm with poor FPR to reject obvious mismatches.
Ex. BLAST (sequence alignment) in bioinformatics, followed by slow accurate structure alignment technique.
- K. Dillon and Y.-P. Wang, “On efficient meta-filtering of big data”, 2016
Correlation screening
- Fan, Jianqing, and Jinchi Lv. "Sure independence screening for ultrahigh dimensional feature space." Journal of the Royal Statistical Society: Series B (Statistical Methodology) 70.5 (2008): 849-911.
- Wu, Tong Tong, Yi Fang Chen, Trevor Hastie, Eric Sobel, and Kenneth Lange. "Genome-wide association analysis by lasso penalized logistic regression." Bioinformatics 25.6 (2009): 714-721.
SAFE screening
- Ghaoui, Laurent El, Vivian Viallon, and Tarek Rabbani. "Safe feature elimination for the lasso and sparse supervised learning problems." arXiv preprint arXiv:1009.4219 (2010).
- Liu, Jun, et al. "Safe screening with variational inequalities and its application to lasso." arXiv preprint arXiv:1307.7577 (2013).
Rather than match vs no match, we now need a similarity score a.k.a. distance $d$(string1, string2)
Matching time-series with varying timescales¶
How similar are these two curves, assuming we ignore varying timescales?
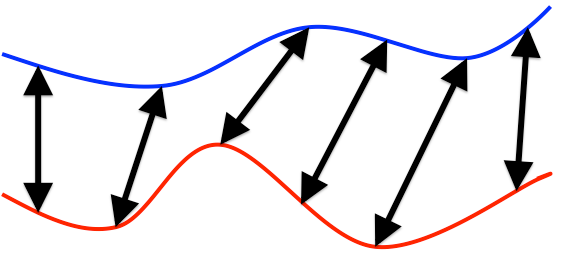
Example: we wish to determine location of hiker given altitude measurements during hike.
Note the amount of warping is often not the distance metric. We first "warp" the pattern, then compute distance some other way, e.g. LMS. Final distance as the closest LMS possible over all acceptable warpings.
Dynamic Time Warping
Dynamic Programming Review¶
Fibonacci sequence¶
\begin{align} f(n) &= f(n-1) + f(n-2) \\ f(0) &= 0 \\ f(1) &= 1 \\ \end{align}
Recursive calculation¶
Inefficient due to repeatedly calculating same terms
def fib_recursive(n):
if n == 0: return 0
if n == 1: return 1
return fib_recursive(n-1) + fib_recursive(n-2)
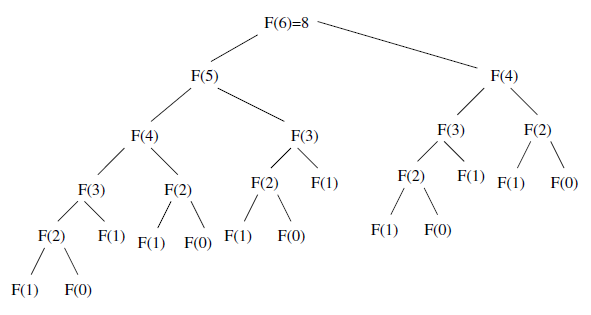
Each term requires two additional terms be calculated. Exponential time.
DP calculation¶
Intelligently plan terms to calculate and store ("cache"), e.g. in a table.
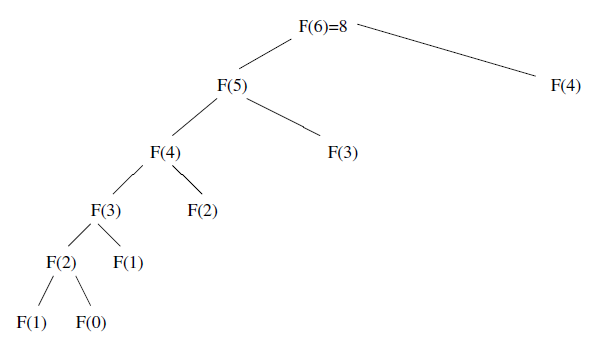
Each term requires one term be calculated.
DP Caching¶
Always plan out the data structure and calculation order.
- need to make sure you have sufficient space
- need to choose optimal strategy to fill in
The data structure to fill in for Fibonacci is trivial:

Optimal order is to start at bottom and work up to $n$, so always have what you need for next term.
What are caches?¶
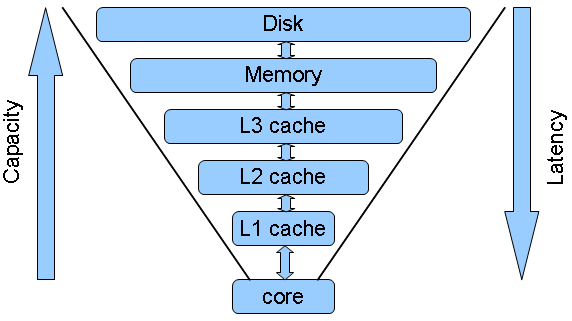
Caches are storage for information to be used in the near future in a more accessible form.
The difference between dynamic programming and recursion¶
1) Direction
Recursion: Starts at the end/largest and divides into subproblems.
DP: Starts at the smallest and builds up a solution.
2) Amount of computation:
During recursion, the same sub-problems are solved multiple times.
DP is basically a memoization technique which uses a table to store the results of sub-problem so that if same sub-problem is encountered again in future, it could directly return the result instead of re-calculating it.
DP = apply common sense to do recursive problems more efficiently.
def fib_recursive(n):
if n == 0: return 0
if n == 1: return 1
return fib_recursive(n-1) + fib_recursive(n-2)
def fib_dp(n):
fib_seq = [0, 1]
for i in range(2,n+1):
fib_seq.append(fib_seq[i-1] + fib_seq[i-2])
return fib_seq[n]
Let's compare the runtime
%timeit -n4 fib_recursive(30)
390 ms ± 25.3 ms per loop (mean ± std. dev. of 7 runs, 4 loops each)
%timeit -n4 fib_dp(100)
14.5 µs ± 1.79 µs per loop (mean ± std. dev. of 7 runs, 4 loops each)
Important Point¶
The hardest parts of dynamic programming is:
- Recognizing when to use it
- Picking the right data structure for caching
Generator approach¶
def fib():
a, b = 0, 1
while True:
a, b = b, a+b
yield a
f = fib()
for i in range(10):
print(next(f))
1 1 2 3 5 8 13 21 34 55
from itertools import islice
help(islice)
Help on class islice in module itertools: class islice(builtins.object) | islice(iterable, stop) --> islice object | islice(iterable, start, stop[, step]) --> islice object | | Return an iterator whose next() method returns selected values from an | iterable. If start is specified, will skip all preceding elements; | otherwise, start defaults to zero. Step defaults to one. If | specified as another value, step determines how many values are | skipped between successive calls. Works like a slice() on a list | but returns an iterator. | | Methods defined here: | | __getattribute__(self, name, /) | Return getattr(self, name). | | __iter__(self, /) | Implement iter(self). | | __next__(self, /) | Implement next(self). | | __reduce__(...) | Return state information for pickling. | | __setstate__(...) | Set state information for unpickling. | | ---------------------------------------------------------------------- | Static methods defined here: | | __new__(*args, **kwargs) from builtins.type | Create and return a new object. See help(type) for accurate signature.
n = 100
next(islice(fib(), n-1, n))
354224848179261915075
%timeit -n4 next(islice(fib(), n-1, n))
The slowest run took 9.46 times longer than the fastest. This could mean that an intermediate result is being cached. 21.7 µs ± 28.4 µs per loop (mean ± std. dev. of 7 runs, 4 loops each)
Memoization¶
A technique used in computing to speed up programs. Temporarily stores the calculation results of processed input such as the results of function calls.
If the same input or a function call with the same parameters is used, the previously stored results can be used again and unnecessary calculation are avoided.
In many cases a simple array is used for storing the results, but lots of other structures can be used as well, such as associative arrays, called hashes in Perl or dictionaries in Python.
Source: http://www.amazon.com/Algorithm-Design-Manual-Steve-Skiena/dp/0387948600
def fib_recursive(n):
if n == 0: return 0
if n == 1: return 1
return fib_recursive(n-1) + fib_recursive(n-2)
def fib_dp(n):
cache = [0,1]
for i in range(2,n+1):
cache.append(cache[i-1]+cache[i-2])
return cache[n]
def memoize(f):
memo = {}
def helper(x):
if x not in memo:
memo[x] = f(x)
return memo[x]
return helper
fib_recursive_memoized = memoize(fib_recursive)
fib_recursive_memoized(9)
34
%timeit fib_recursive(9)
6.23 μs ± 177 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
%timeit fib_recursive_memoized(9)
80.7 ns ± 1.49 ns per loop (mean ± std. dev. of 7 runs, 10,000,000 loops each)
from functools import lru_cache
@lru_cache()
def fib_recursive(n):
"Calculate nth Fibonacci number using recursion"
if n == 0: return 0
if n == 1: return 1
return fib_recursive(n-1) + fib_recursive(n-2)
%timeit fib_recursive(n)
55 ns ± 1.69 ns per loop (mean ± std. dev. of 7 runs, 10,000,000 loops each)
Memoization in Python with joblib¶
import joblib
dir(joblib)
['Logger', 'MemorizedResult', 'Memory', 'Parallel', 'PrintTime', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__path__', '__spec__', '__version__', '_cloudpickle_wrapper', '_memmapping_reducer', '_multiprocessing_helpers', '_parallel_backends', '_store_backends', '_utils', 'backports', 'compressor', 'cpu_count', 'delayed', 'disk', 'dump', 'effective_n_jobs', 'executor', 'expires_after', 'externals', 'func_inspect', 'hash', 'hashing', 'load', 'logger', 'memory', 'numpy_pickle', 'numpy_pickle_compat', 'numpy_pickle_utils', 'os', 'parallel', 'parallel_backend', 'parallel_config', 'pool', 'register_compressor', 'register_parallel_backend', 'register_store_backend', 'wrap_non_picklable_objects']
Exercise: Change making problem.¶
The objective is to determine the smallest number of currency of a particular denomination required to make change for a given amount.
For example, if the denomination of the currency are \$1 and \$2 and it was required to make change for \$3 then we would use \$1 + \$2 i.e. 2 pieces of currency.
However if the amount was \$4 then we would could either use \$1+\$1+\$1+\$1 or \$1+\$1+\$2 or \$2+\$2 and the minimum number of currency would 2 (\$2+\$2).

Solution: dynamic programming (DP).¶
The minimum number of coins required to make change for \$P is the number of coins required to make change for the amount \$P-x plus 1 (+1 because we need another coin to get us from \$P-x to P).
These can be illustrated mathematically as:
Let us assume that we have $n$ currency of distinct denomination. Where the denomination of the currency $i$ is $v_i$. We can sort the currency according to denomination values such that $v_1<v_2<v_3<..<v_n$
Let us use $C(p)$ to denote the minimum number of currency required to make change for $ \$p$
Using the principles of recursion $C(p)=min_i C(p-v_i)+1$
For example, assume we want to make 5, and $v_1=1, v_2=2, v_3=3$.
Therefore $C(5) = min(C(5-1)+1, C(5-2)+1, C(5-3)+1)$ $\Longrightarrow min(C(4)+1, C(3)+1, C(2)+1)$
Exercise: Compute a polynomial over a list of points¶
How can we use redundancy here?
Mini-summary¶
In a recursive approach, your function recursively calls itself on smaller subproblems as needed, until the calculation is done. Potentially performing many redundant calculations naively.
With memoization, you form a cache of these recursive calls, and check if the same one is called again before recalculating. Still potential danger since do not plan memory needs or usage.
With Dynamic Programming, you follow a bottum-up plan to produce the cache of results for smaller subproblems.
Edit Distance between two strings¶
Minimum number of operations needed to convert one string into other
Ex. typo correction: how do we decide what "scool" was supposed to be?
Consider possibilities with lowest edit distance. "school" or "cool".
Hamming distance - operations consist only of substitutions of character (i.e. count differences)
Levenshtein distance - operations are the removal, insertion, or substitution of a character
"Fuzzy String Matching"
def hammingDistance(x, y):
''' Return Hamming distance between x and y '''
assert len(x) == len(y)
nmm = 0
for i in range(0, len(x)):
if x[i] != y[i]:
nmm += 1
return nmm
hammingDistance('brown', 'blown')
1
hammingDistance('cringe', 'orange')
2
Levenshtein distance (between strings $P$ and $T$)¶
Special case where the operations are the insertion, deletion, or substitution of a character
- Insertion – Insert a single character into pattern $P$ to help it match text $T$ , such as changing “ago” to “agog.”
- Deletion – Delete a single character from pattern $P$ to help it match text $T$ , such as changing “hour” to “our.”
- Substitution – Replace a single character from pattern $P$ with a different character in text $T$ , such as changing “shot” to “spot.”
Count the minimum number needed to convert $P$ into $T$.
Interchangably called "edit distance".
Exercise: What are the Hamming and Edit distances?¶
\begin{align} T: \text{"The quick brown fox"} \\ P: \text{"The quick grown fox"} \\ \end{align}
\begin{align} T: \text{"The quick brown fox"} \\ P: \text{"The quik brown fox "} \\ \end{align}
Exercise: What are the Edit distances?¶
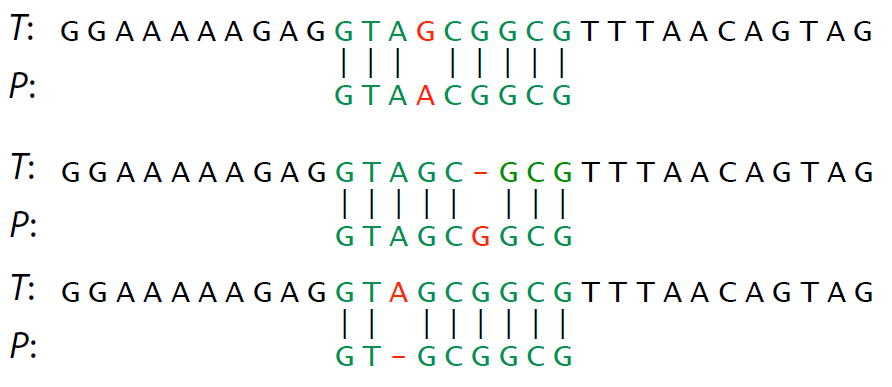
Comprehension check: give three different ways to transform $P$ into $T$ (not necessarily fewest operations)
Edit distance - Divide and conquer¶
How do we use simpler comparisons to perform more complex ones?
Use substring match results to compute
Consider by starting from first character and building up
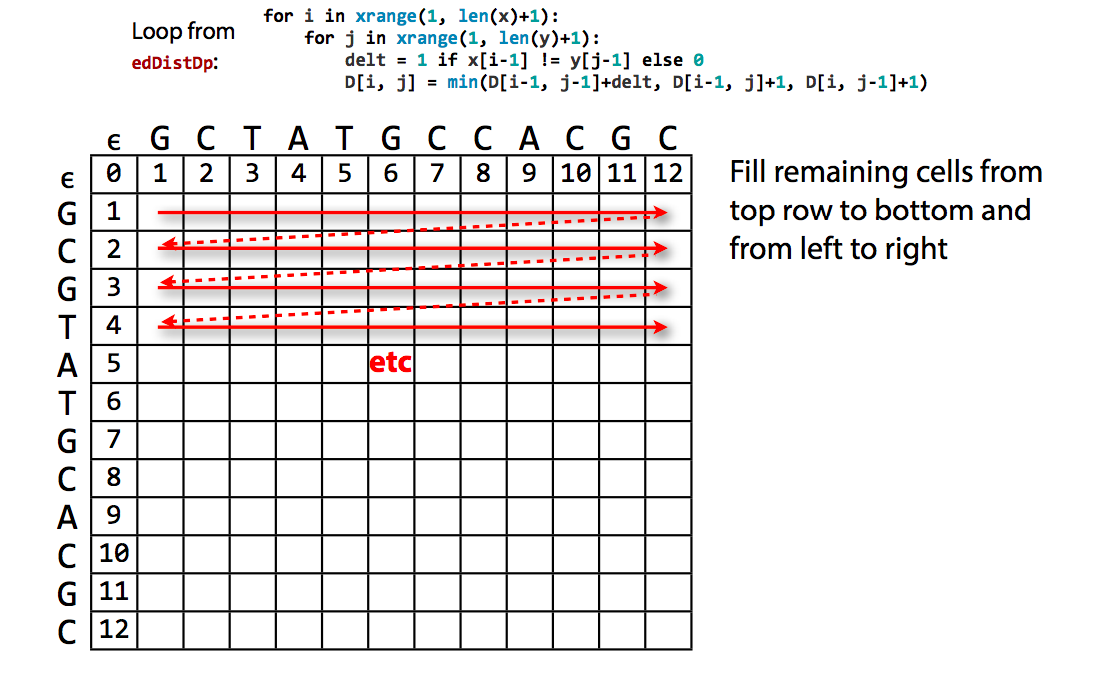
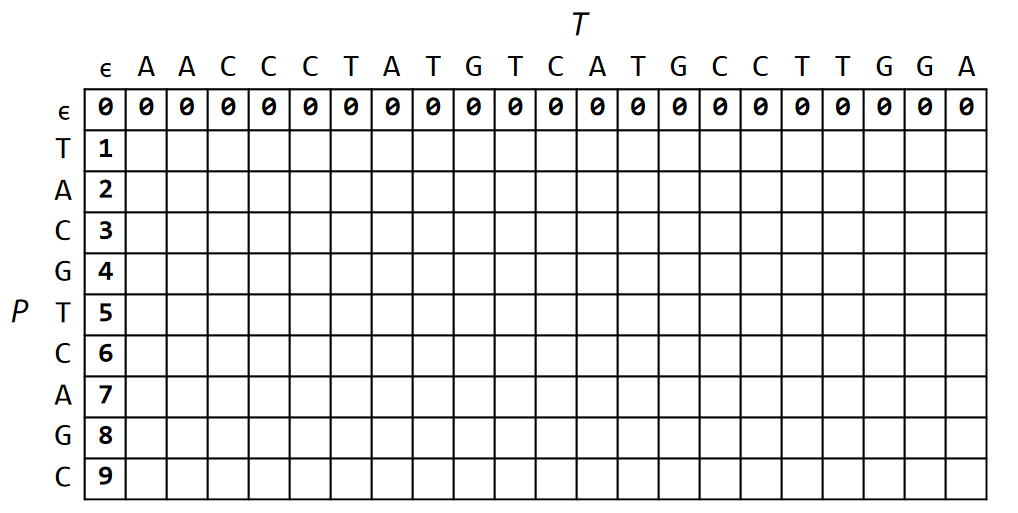
The DP matrix¶
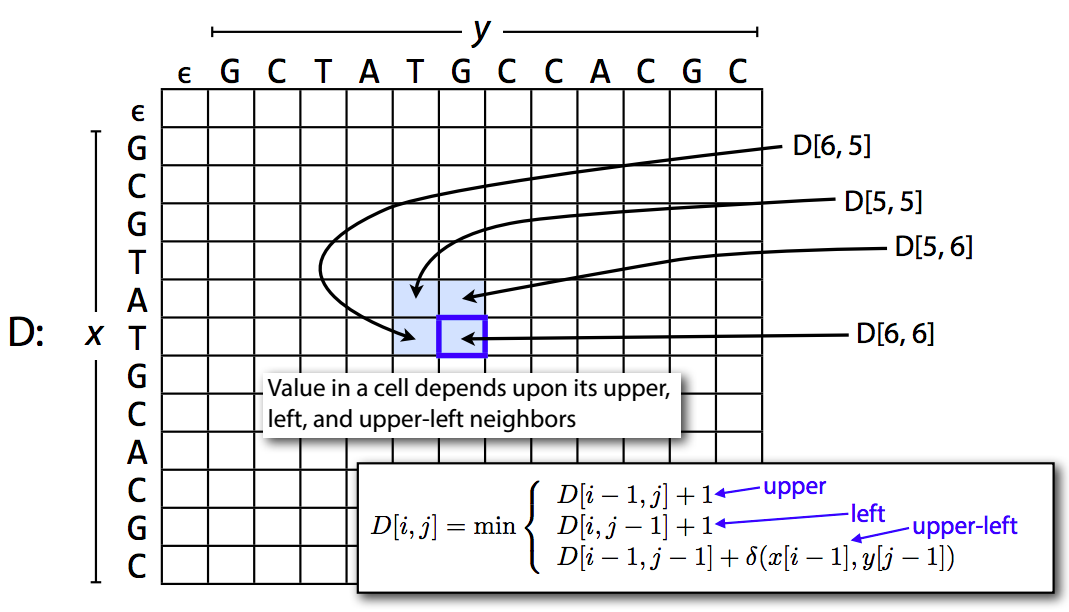
Initialization¶

Computation¶
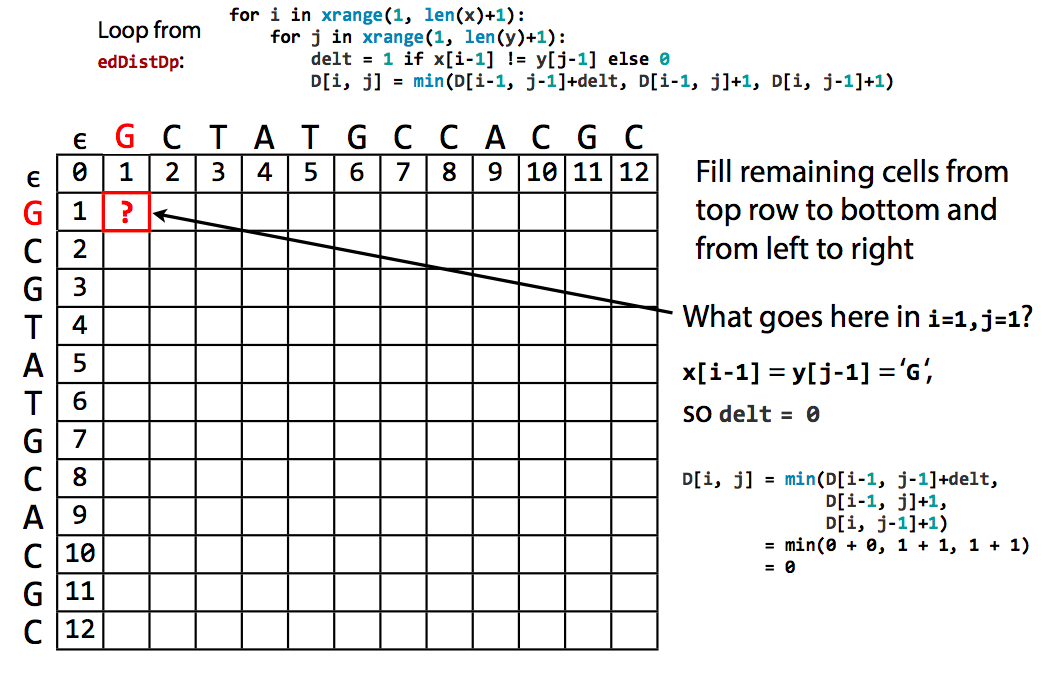
Final edit distance is lower right corner¶
Comparison of entirety of both strings

So the net result tells us the minimum number of operations is 2. But what are they?
Traceback: the minimum "edit"¶
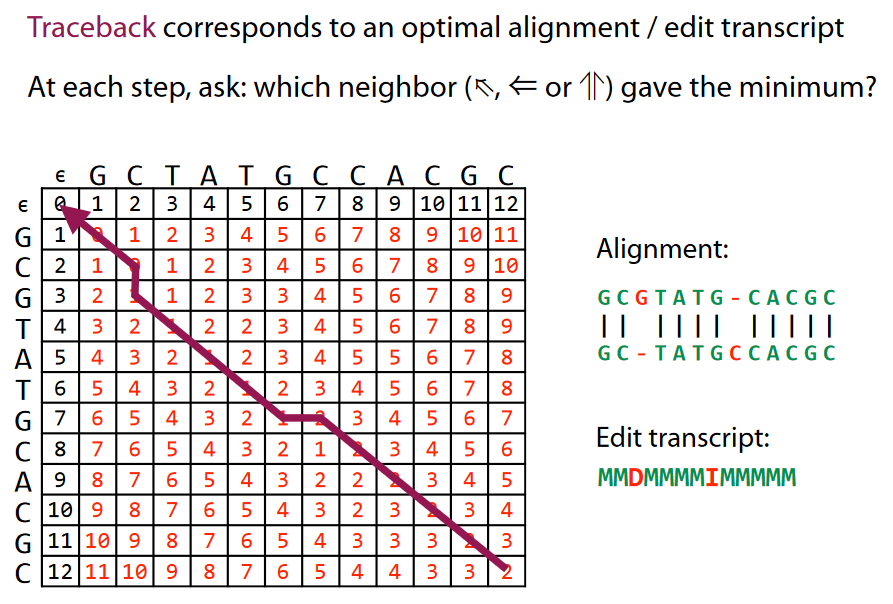
- Diagonal = Match (M) or Substitution (S) - depending if distance increased while following diagonal or remained constant
- Vertical = Deletion (D)
- Horizontal = Insertion (I)
Traceback: the minimum "edit"¶

- Diagonal = Match (M) or Substitution (S) - depending if distance increased while following diagonal or remained constant
- Vertical = Deletion (D)
- Horizontal = Insertion (I)
see http://www.cs.jhu.edu/~langmea/resources/lecture_notes/dp_and_edit_dist.pdf for more details
Note: use of (I) vs. (D) here depends which of the two strings you are editing to become the other
Note II: an error in backtrace line in picture, can you find it?
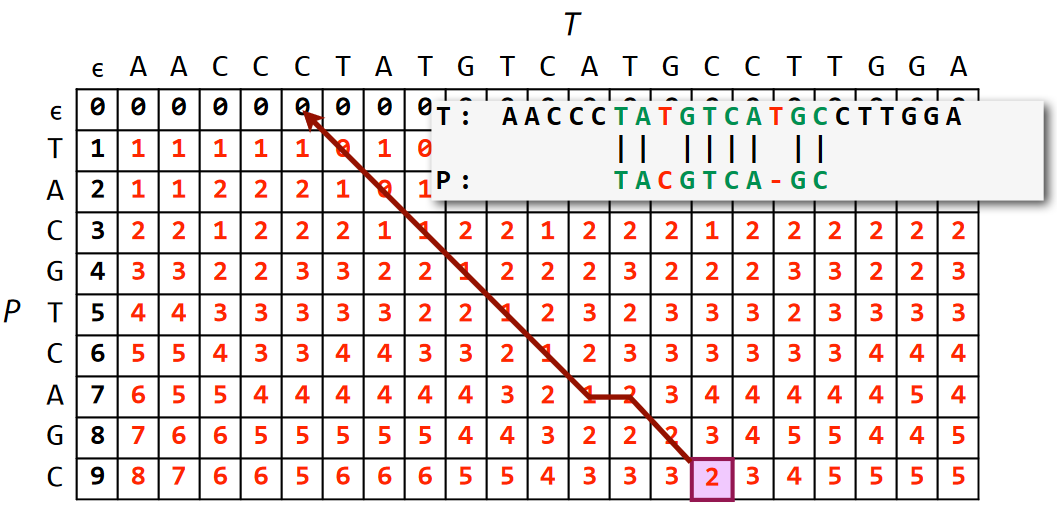
Traceback is a form of diff¶
Storing just diffs reduces storage amount.
For example, git
Seek lowest difference on bottom row, endpoint of substring in $T$.
def edDistRecursive(x, y):
if len(x) == 0: return len(y)
if len(y) == 0: return len(x)
delt = 1 if x[-1] != y[-1] else 0
vert = edDistRecursive(x[:-1], y) + 1
horz = edDistRecursive(x, y[:-1]) + 1
diag = edDistRecursive(x[:-1], y[:-1]) + delt
return min(diag, vert, horz)
edDistRecursive('Shakespeare', 'shake spear') # this takes a while!
3
Memoized version¶
def edDistRecursiveMemo(x, y, memo=None):
''' A version of edDistRecursive with memoization. For each x, y we see, we
record result from edDistRecursiveMemo(x, y). In the future, we retrieve
recorded result rather than re-run the function. '''
if memo is None: memo = {}
if len(x) == 0: return len(y)
if len(y) == 0: return len(x)
if (len(x), len(y)) in memo:
return memo[(len(x), len(y))]
delt = 1 if x[-1] != y[-1] else 0
diag = edDistRecursiveMemo(x[:-1], y[:-1], memo) + delt
vert = edDistRecursiveMemo(x[:-1], y, memo) + 1
horz = edDistRecursiveMemo(x, y[:-1], memo) + 1
ans = min(diag, vert, horz)
memo[(len(x), len(y))] = ans
return ans
edDistRecursiveMemo('Shakespeare', 'shake spear') # this is very fast
3
DP version¶
from numpy import zeros
def edDistDp(x, y):
""" Calculate edit distance between sequences x and y using
matrix dynamic programming. Return distance. """
D = zeros((len(x)+1, len(y)+1), dtype=int)
D[0, 1:] = range(1, len(y)+1)
D[1:, 0] = range(1, len(x)+1)
for i in range(1, len(x)+1):
for j in range(1, len(y)+1):
delt = 1 if x[i-1] != y[j-1] else 0
D[i, j] = min(D[i-1, j-1]+delt, D[i-1, j]+1, D[i, j-1]+1)
return D[len(x), len(y)]
edDistDp('Shakespeare', 'shake spear')
3
Levenshtein Demo¶
Check for Understanding¶
What are the givens for DP?
- A map
- A goal
What is the output of DP?
Best "path" from any "location" - meaning what?
How is the value calculated in DP?
It is the min/max of:
- The previous max
- The current value
How does DP generate the best "path"?
Start at goal and calculate the value function for every step all the path back to start
Mini-Summary (take 2?)¶
- Dynamic programming is a improved version of recrusion
- Dynamic programming uses caches to save compute, storing the results of previous calculations in a systematic way for later use
- Backtrace is storing the diff for later use.
Further Improvement/Optimization¶
Many more specialized algorithms exist in the fields DP is used.
DP is a category of methods, not a single method.
Can you think of ways to perform these tasks faster?
Plan B. Be even more clever about intermediate calculations. E.g. compute table in way more likely to find optimal sooner (before filling entire table).
Plan A. "good" approximations (hopefully). E.g. computing a match based on only short substrings, not entire string.
Matching time series: Dynamic Time Warping¶
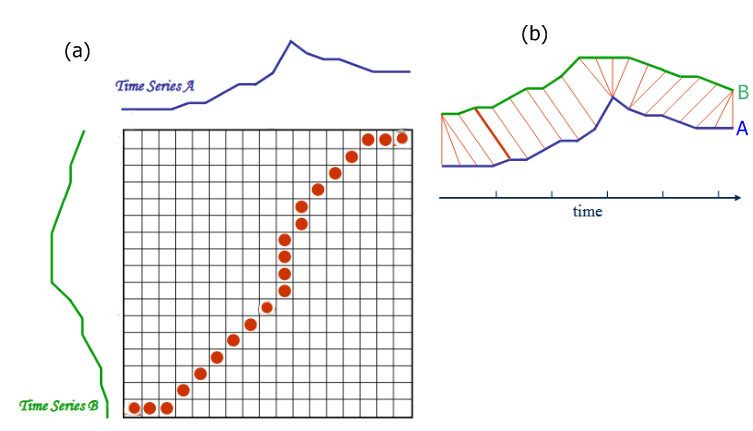
Generally similar to edit distance algorithm, except we compute a function $d()$ at each comparison
import numpy as np
# define whatever distance metric you want
def d(x,y):
return abs(x-y)
# the DP DWT distance algorithm
def DTWDistance(A, B):
n = len(A)
m = len(B)
DTW = np.zeros((n,m))
for i in range(0,n):
for j in range(0,m):
DTW[i, j] = np.inf
DTW[0, 0] = 0
for i in range(1,n):
for j in range(1,m):
cost = d(A[i], B[j])
DTW[i, j] = cost + min((DTW[i-1, j ], # insertion
DTW[i , j-1], # deletion
DTW[i-1, j-1])) # match
print(DTW)
return DTW[n-1, m-1]
DTWDistance([1,2,3],[1,3,3,3,3])
[[ 0. inf inf inf inf] [inf 1. 2. 3. 4.] [inf 1. 1. 1. 1.]]
1.0