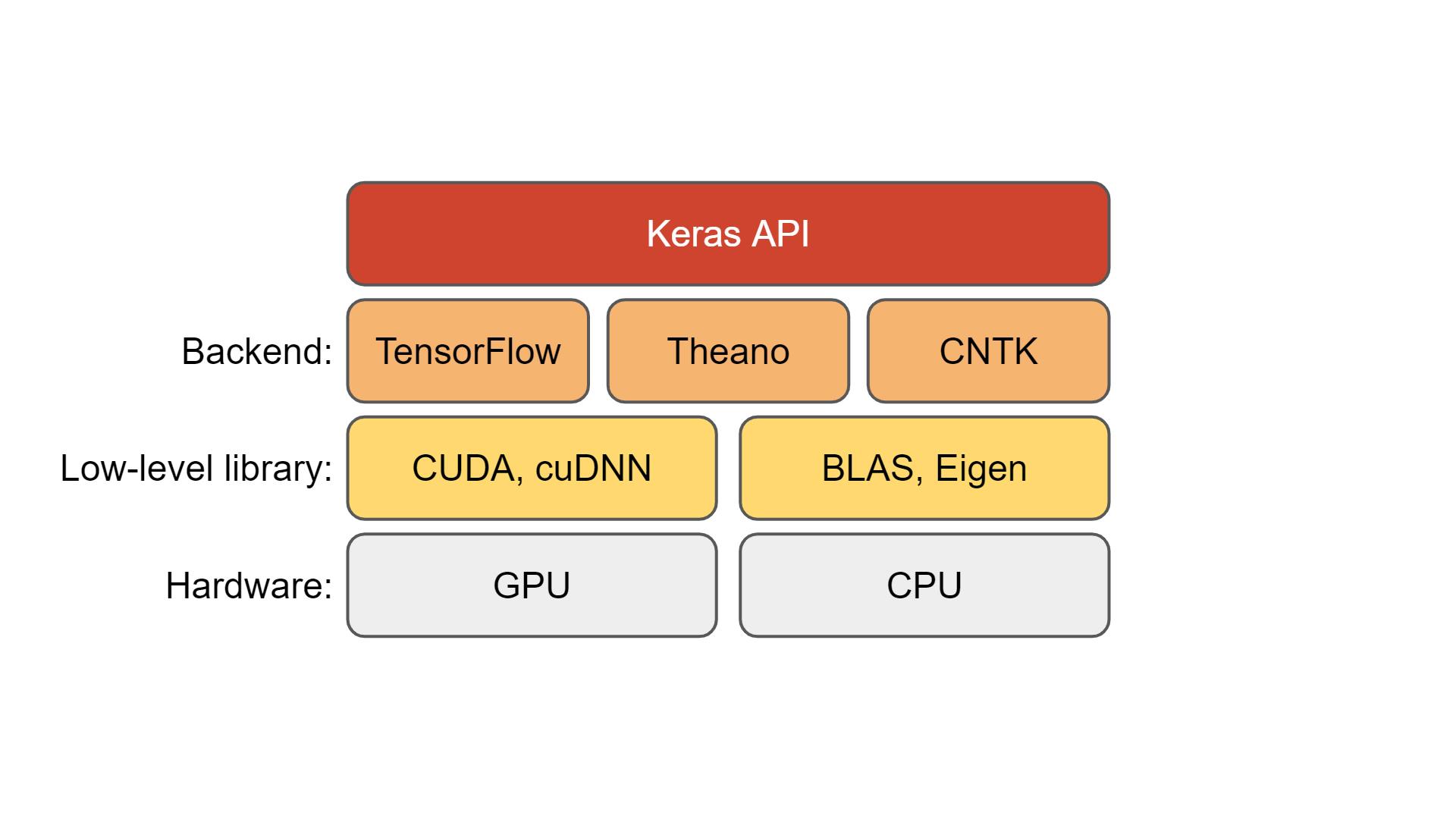
Mathematical Methods for Data Science

Topic 5: "Classical" Linear Algebra Software
This topic:¶
- BLAS, LAPACK, Eigen
- Overview of major python packages
- Numpy practice
Reading: the internet
What is "Classical" Linear Algebra software?¶
- A term I just invented
- Originally single CPU, RAM-limited implementations of well-known algorithms (e.g. Golub & Van Loan "Matrix Computations")
- ...and higher-level packages based on these algorithms, inheriting the limitations
- Large-scale (more than 10k variable or so) only possible via sparse linear algebra algorithms
- Leading parallel tool is SIMD (single instruction multiple data) via math co-processors.
- More parallelism at top-level rather than bottom ("workers" running seperate processes on separate CPU's)
- Updates based on producing variants rather than complete replacement
I. BLAS BLAS BLAS¶
BLAS = Basic Linear Algebra Subprograms¶
"Building block" algorithms for matrix algebra
- scaling, multiplying. "Level 1,2,3 functions"
- single and double precision, real and complex numbers
- generally don't take advantage of multiple threads or CPU's by chip maker
- Are often optimized for complex instructions however, e.g. SIMD
- Originally FORTRAN - one-based, columns first, like matlab
- various implementations, including parallelizable versions, C/C++ CUDA,
- http://www.netlib.org/blas/
More Implementations¶
- cuBLAS - NVIDIA https://developer.nvidia.com/cublas
- rocBLAS - AMD https://github.com/ROCm/rocBLAS?tab=readme-ov-file
- clBLAS, CLBlast - OpenCL https://github.com/CNugteren/CLBlast
- hipBLAS - a wrapper around other BLAS implementations https://github.com/ROCm/hipBLAS
- gotoBLAS, BLIS, OpenBLAS - optimized implementations for CPU https://en.wikipedia.org/wiki/GotoBLAS, https://www.openblas.net/, https://github.com/flame/blis
cuBLAS: Basic Linear Algebra on NVIDIA GPUs¶
https://developer.nvidia.com/cublas
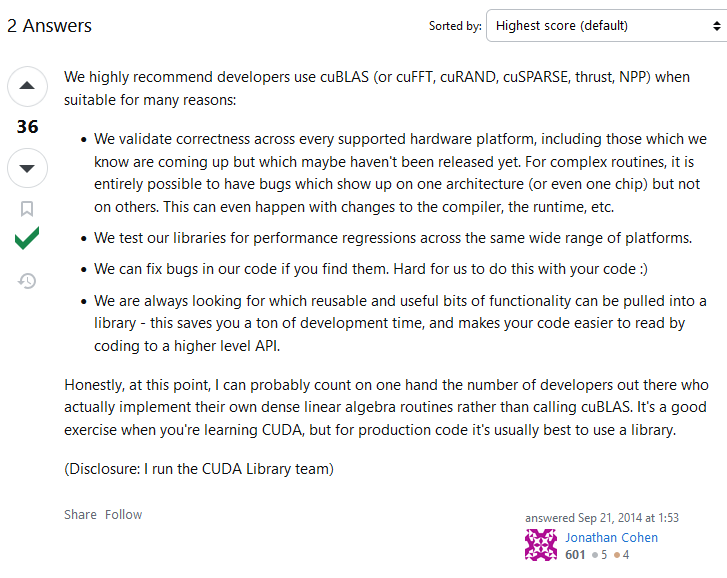
https://stackoverflow.com/questions/25836003/normal-cuda-vs-cublas
BLAS Levels 1,2,3 ~ $O(n), O(n^2), O(n^3)$¶

import scipy.linalg.blas as blas
printcols(dir(blas),6)
HAS_ILP64 chemm daxpy dtrmv sspmv zhbmv __all__ chemv dcopy dtrsm sspr zhemm __builtins__ cher ddot dtrsv sspr2 zhemv __cached__ cher2 dgbmv dzasum sswap zher __doc__ cher2k dgemm dznrm2 ssymm zher2 __file__ cherk dgemv find_best_blas_type ssymv zher2k __loader__ chpmv dger functools ssyr zherk __name__ chpr dnrm2 get_blas_funcs ssyr2 zhpmv __package__ chpr2 drot icamax ssyr2k zhpr __spec__ crotg drotg idamax ssyrk zhpr2 _blas_alias cscal drotm isamax stbmv zrotg _cblas cspmv drotmg izamax stbsv zscal _fblas cspr dsbmv sasum stpmv zspmv _fblas_64 csrot dscal saxpy stpsv zspr _get_funcs csscal dspmv scasum strmm zswap _memoize_get_funcs cswap dspr scnrm2 strmv zsymm _np csymm dspr2 scopy strsm zsyr _type_conv csyr dswap sdot strsv zsyr2k _type_score csyr2k dsymm sgbmv zaxpy zsyrk caxpy csyrk dsymv sgemm zcopy ztbmv ccopy ctbmv dsyr sgemv zdotc ztbsv cdotc ctbsv dsyr2 sger zdotu ztpmv cdotu ctpmv dsyr2k snrm2 zdrot ztpsv cgbmv ctpsv dsyrk srot zdscal ztrmm cgemm ctrmm dtbmv srotg zgbmv ztrmv cgemv ctrmv dtbsv srotm zgemm ztrsm cgerc ctrsm dtpmv srotmg zgemv ztrsv cgeru ctrsv dtpsv ssbmv zgerc chbmv dasum dtrmm sscal zgeru
Recall: Inside the GPU¶
General Matrix Multiplication (GEMM) ~ $C = \alpha AB + \beta C$
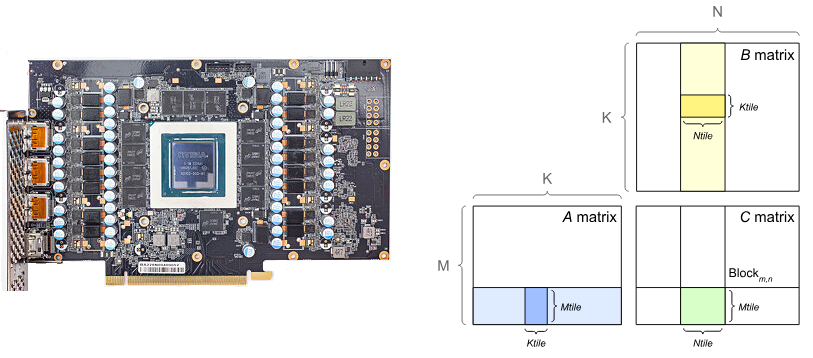
https://docs.nvidia.com/deeplearning/performance/dl-performance-matrix-multiplication/index.html
LAPACK = Linear Algebra Package¶
- Fortran, Uses BLAS as backend (can choose different implementations)
- http://www.netlib.org/lapack/
- https://github.com/Reference-LAPACK/lapack
- systems of simultaneous linear equations
- least-squares solutions of linear systems of equations
- eigenvalue problems
- singular value problems.
- associated matrix factorizations (LU, Cholesky, QR, SVD, Schur, generalized Schur)
- related computations such as reordering of the Schur factorizations and estimating condition numbers.
- Dense and banded matrices are handled, but not general sparse matrices.
- real and complex matrices
- both single and double precision.
- Matlab, and the Python tools we will use were essentially built on this
import scipy.linalg.lapack as lapack
printcols(dir(lapack),6)
HAS_ILP64 clartg dgetc2 dtrsyl ssbev zgttrs _DeprecatedImport claswp dgetrf dtrtri ssbevd zhbevd __all__ clauum dgetri dtrtrs ssbevx zhbevx __builtins__ cpbsv dgetri_lwork dtrttf ssfrk zhecon __cached__ cpbtrf dgetrs dtrttp sstebz zheequb __doc__ cpbtrs dgges dtzrzf sstein zheev __file__ cpftrf dggev dtzrzf_lwork sstemr zheev_lwork __loader__ cpftri dgglse flapack sstemr_lwork zheevd __name__ cpftrs dgglse_lwork get_lapack_funcs ssterf zheevd_lwork __package__ cpocon dgtsv ilaver sstev zheevr __spec__ cposv dgtsvx routine ssycon zheevr_lwork _check_work_float cposvx dgttrf sgbsv ssyconv zheevx _clapack cpotrf dgttrs sgbtrf ssyequb zheevx_lwork _compute_lwork cpotri dlamch sgbtrs ssyev zhegst _flapack cpotrs dlange sgebal ssyev_lwork zhegv _flapack_64 cppcon dlarf sgecon ssyevd zhegv_lwork _get_funcs cppsv dlarfg sgeequ ssyevd_lwork zhegvd _int32_max cpptrf dlartg sgeequb ssyevr zhegvx _int64_max cpptri dlasd4 sgees ssyevr_lwork zhegvx_lwork _lapack_alias cpptrs dlaswp sgeev ssyevx zhesv _memoize_get_funcs cpstf2 dlauum sgeev_lwork ssyevx_lwork zhesv_lwork _np cpstrf dorcsd sgehrd ssygst zhesvx cgbsv cpteqr dorcsd_lwork sgehrd_lwork ssygv zhesvx_lwork cgbtrf cptsv dorghr sgejsv ssygv_lwork zhetrd cgbtrs cptsvx dorghr_lwork sgels ssygvd zhetrd_lwork cgebal cpttrf dorgqr sgels_lwork ssygvx zhetrf cgecon cpttrs dorgrq sgelsd ssygvx_lwork zhetrf_lwork cgeequ crot dormqr sgelsd_lwork ssysv zhfrk cgeequb csycon dormrz sgelss ssysv_lwork zlange cgees csyconv dormrz_lwork sgelss_lwork ssysvx zlarf cgeev csyequb dpbsv sgelsy ssysvx_lwork zlarfg cgeev_lwork csysv dpbtrf sgelsy_lwork ssytf2 zlartg cgehrd csysv_lwork dpbtrs sgemqrt ssytrd zlaswp cgehrd_lwork csysvx dpftrf sgeqp3 ssytrd_lwork zlauum cgels csysvx_lwork dpftri sgeqrf ssytrf zpbsv cgels_lwork csytf2 dpftrs sgeqrf_lwork ssytrf_lwork zpbtrf cgelsd csytrf dpocon sgeqrfp stbtrs zpbtrs cgelsd_lwork csytrf_lwork dposv sgeqrfp_lwork stfsm zpftrf cgelss ctbtrs dposvx sgeqrt stfttp zpftri cgelss_lwork ctfsm dpotrf sgerqf stfttr zpftrs cgelsy ctfttp dpotri sgesc2 stgexc zpocon cgelsy_lwork ctfttr dpotrs sgesdd stgsen zposv cgemqrt ctgexc dppcon sgesdd_lwork stgsen_lwork zposvx cgeqp3 ctgsen dppsv sgesv stpmqrt zpotrf cgeqrf ctgsen_lwork dpptrf sgesvd stpqrt zpotri cgeqrf_lwork ctpmqrt dpptri sgesvd_lwork stpttf zpotrs cgeqrfp ctpqrt dpptrs sgesvx stpttr zppcon cgeqrfp_lwork ctpttf dpstf2 sgetc2 strsyl zppsv cgeqrt ctpttr dpstrf sgetrf strtri zpptrf cgerqf ctrsyl dpteqr sgetri strtrs zpptri cgesc2 ctrtri dptsv sgetri_lwork strttf zpptrs cgesdd ctrtrs dptsvx sgetrs strttp zpstf2 cgesdd_lwork ctrttf dpttrf sgges stzrzf zpstrf cgesv ctrttp dpttrs sggev stzrzf_lwork zpteqr cgesvd ctzrzf dsbev sgglse zgbsv zptsv cgesvd_lwork ctzrzf_lwork dsbevd sgglse_lwork zgbtrf zptsvx cgesvx cuncsd dsbevx sgtsv zgbtrs zpttrf cgetc2 cuncsd_lwork dsfrk sgtsvx zgebal zpttrs cgetrf cunghr dstebz sgttrf zgecon zrot cgetri cunghr_lwork dstein sgttrs zgeequ zsycon cgetri_lwork cungqr dstemr slamch zgeequb zsyconv cgetrs cungrq dstemr_lwork slange zgees zsyequb cgges cunmqr dsterf slarf zgeev zsysv cggev cunmrz dstev slarfg zgeev_lwork zsysv_lwork cgglse cunmrz_lwork dsycon slartg zgehrd zsysvx cgglse_lwork dgbsv dsyconv slasd4 zgehrd_lwork zsysvx_lwork cgtsv dgbtrf dsyequb slaswp zgels zsytf2 cgtsvx dgbtrs dsyev slauum zgels_lwork zsytrf cgttrf dgebal dsyev_lwork sorcsd zgelsd zsytrf_lwork cgttrs dgecon dsyevd sorcsd_lwork zgelsd_lwork ztbtrs chbevd dgeequ dsyevd_lwork sorghr zgelss ztfsm chbevx dgeequb dsyevr sorghr_lwork zgelss_lwork ztfttp checon dgees dsyevr_lwork sorgqr zgelsy ztfttr cheequb dgeev dsyevx sorgrq zgelsy_lwork ztgexc cheev dgeev_lwork dsyevx_lwork sormqr zgemqrt ztgsen cheev_lwork dgehrd dsygst sormrz zgeqp3 ztgsen_lwork cheevd dgehrd_lwork dsygv sormrz_lwork zgeqrf ztpmqrt cheevd_lwork dgejsv dsygv_lwork spbsv zgeqrf_lwork ztpqrt cheevr dgels dsygvd spbtrf zgeqrfp ztpttf cheevr_lwork dgels_lwork dsygvx spbtrs zgeqrfp_lwork ztpttr cheevx dgelsd dsygvx_lwork spftrf zgeqrt ztrsyl cheevx_lwork dgelsd_lwork dsysv spftri zgerqf ztrtri chegst dgelss dsysv_lwork spftrs zgesc2 ztrtrs chegv dgelss_lwork dsysvx spocon zgesdd ztrttf chegv_lwork dgelsy dsysvx_lwork sposv zgesdd_lwork ztrttp chegvd dgelsy_lwork dsytf2 sposvx zgesv ztzrzf chegvx dgemqrt dsytrd spotrf zgesvd ztzrzf_lwork chegvx_lwork dgeqp3 dsytrd_lwork spotri zgesvd_lwork zuncsd chesv dgeqrf dsytrf spotrs zgesvx zuncsd_lwork chesv_lwork dgeqrf_lwork dsytrf_lwork sppcon zgetc2 zunghr chesvx dgeqrfp dtbtrs sppsv zgetrf zunghr_lwork chesvx_lwork dgeqrfp_lwork dtfsm spptrf zgetri zungqr chetrd dgeqrt dtfttp spptri zgetri_lwork zungrq chetrd_lwork dgerqf dtfttr spptrs zgetrs zunmqr chetrf dgesc2 dtgexc spstf2 zgges zunmrz chetrf_lwork dgesdd dtgsen spstrf zggev zunmrz_lwork chfrk dgesdd_lwork dtgsen_lwork spteqr zgglse clange dgesv dtpmqrt sptsv zgglse_lwork clapack dgesvd dtpqrt sptsvx zgtsv clarf dgesvd_lwork dtpttf spttrf zgtsvx clarfg dgesvx dtpttr spttrs zgttrf
C++ API¶
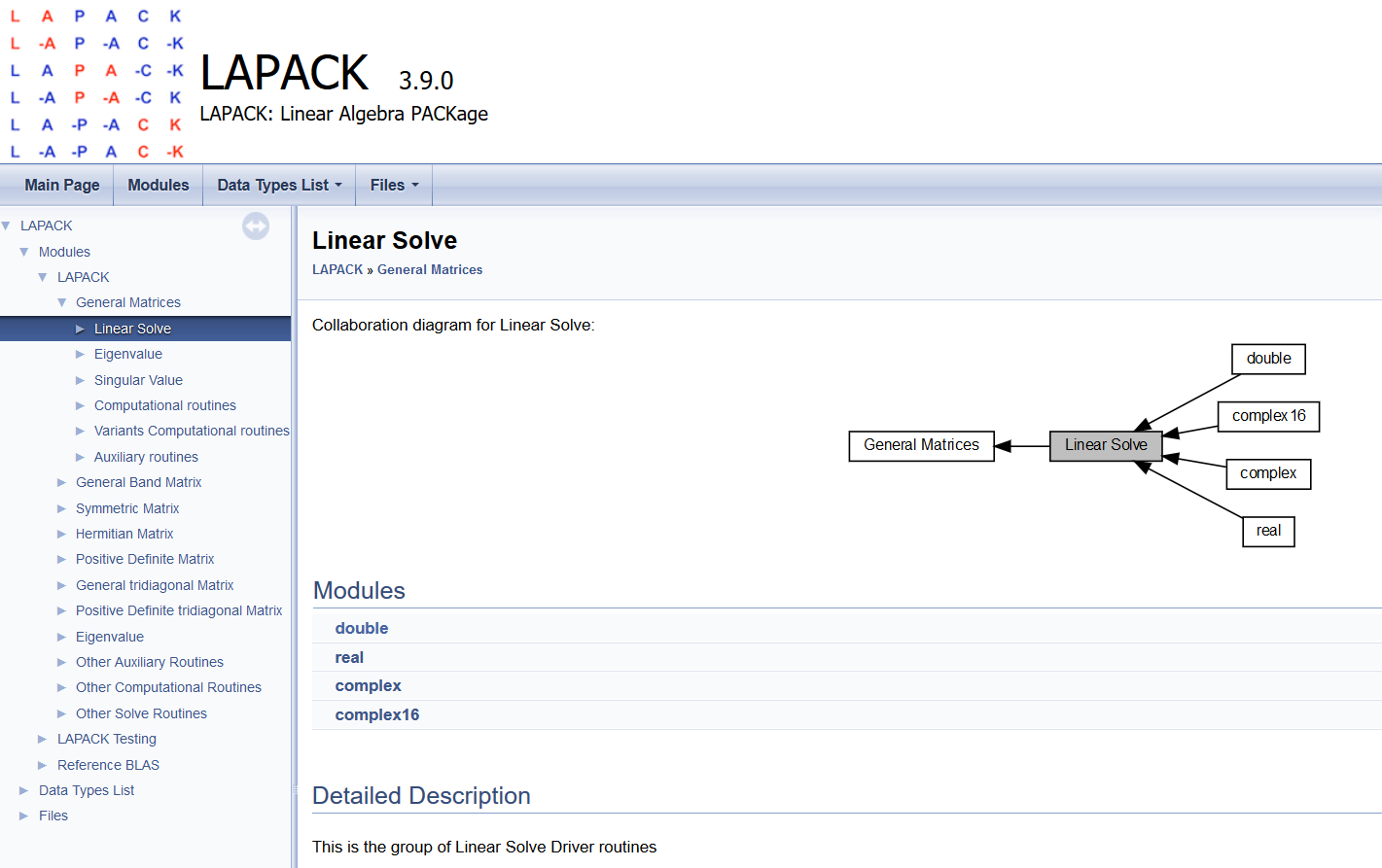
Scipy wrapper API¶
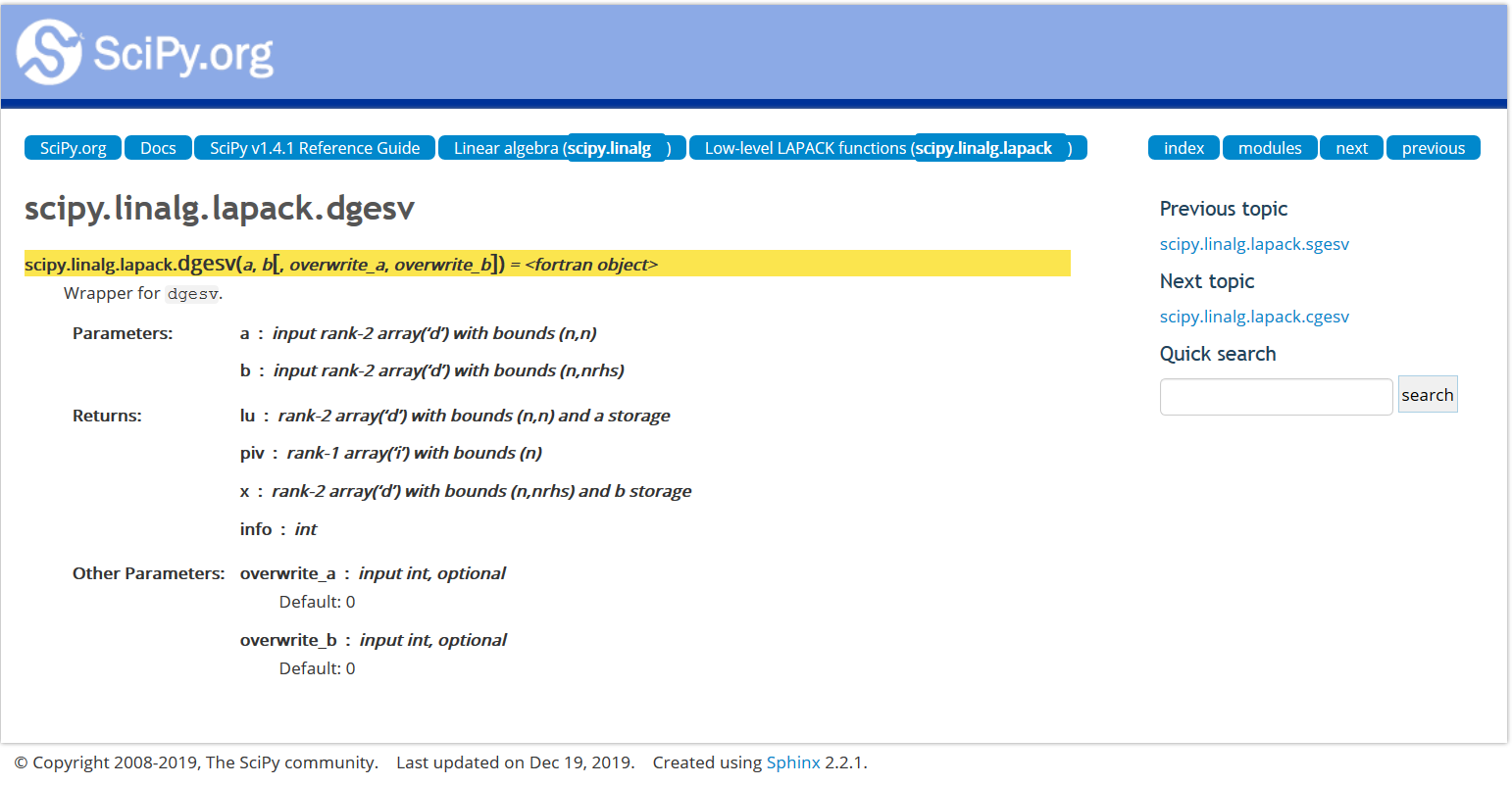
Eigen¶
- https://eigen.tuxfamily.org/dox/
- Written in C++
- Previously used for linear algebra in Tensorflow (single CPU variant probably)
- Low and high-level (e.g. matrix decompositions) linear algebra functions
- Sparse linear algebra
- Can use BLAS/LaPACK as a backend https://eigen.tuxfamily.org/dox/TopicUsingBlasLapack.html
...name can be annoyingly google-proof however
Take-home message¶
Much (most) code you get for free, or even pay for, that implements mathematical algorithms may be of limited value.
Linear algebra, however, is "solved", in terms of numerical programming.
Your main concern is to find an implementation that fits for your application. E.g. parallel, or sparse, or optimized for a particular CPU.
Lab: Import and directly use packages in Python¶
- BLAS - compute a dot product of two random vectors
- LaPACK - solve a random linear system
II. Overview of leading Python tools¶
Leading Python tools:¶
Jupyter - "notebooks" for inline code + LaTex math + markup, etc.
NumPy - low-level array & matrix handling and algorithms
SciPy - higher level numerical algorithms (still fairly basic)
Matplotlib - matlab-style plotting & image display
SkLearn - (Scikit-learn) Machine Learning library
NumPy (short version)¶
- Numerical algorithm toolbox
- Similar to Matlab but Many key differences, such as zero-based indexing (like C) instead of one-based (like math texts).
- Uses BLAS/LAPACK typically
- NumPy Arrays - special data structure which allows direct and efficient linear algebra manipulations (basically a list with added functionality).
import numpy as np
x = np.array([2,0,1,8])
print(x)
[2 0 1 8]
Fast Numerical Mathematics¶
l = range(1234)
%timeit [i ** 2 for i in l]
389 µs ± 8.15 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
import numpy as np
a = np.arange(1234)
%timeit a ** 2
1.41 µs ± 7.46 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
NumPy for Matlab Users¶
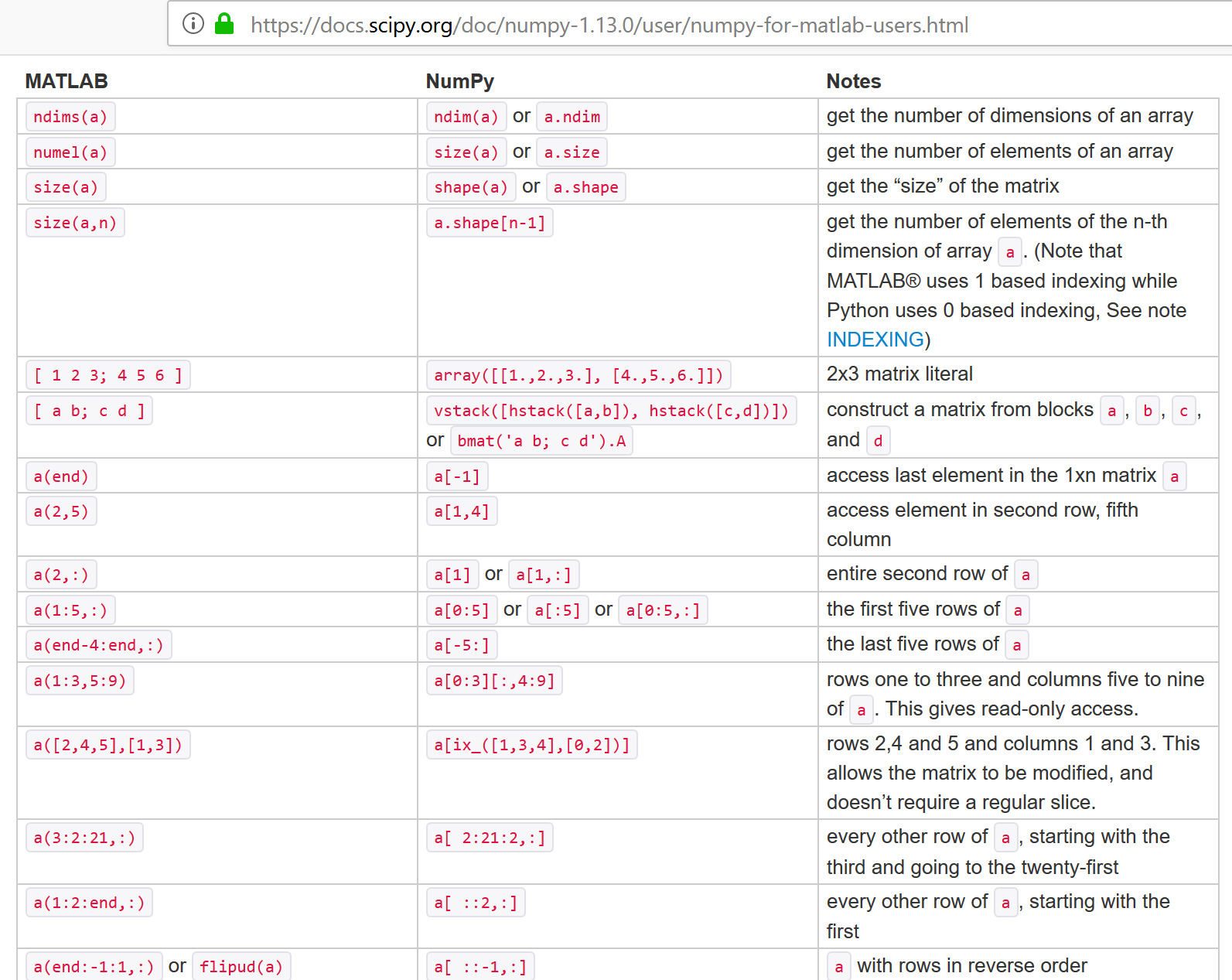
help(np.array)
Help on built-in function array in module numpy.core.multiarray:
array(...)
array(object, dtype=None, copy=True, order='K', subok=False, ndmin=0)
Create an array.
Parameters
----------
object : array_like
An array, any object exposing the array interface, an object whose
__array__ method returns an array, or any (nested) sequence.
dtype : data-type, optional
The desired data-type for the array. If not given, then the type will
be determined as the minimum type required to hold the objects in the
sequence. This argument can only be used to 'upcast' the array. For
downcasting, use the .astype(t) method.
copy : bool, optional
If true (default), then the object is copied. Otherwise, a copy will
only be made if __array__ returns a copy, if obj is a nested sequence,
or if a copy is needed to satisfy any of the other requirements
(`dtype`, `order`, etc.).
order : {'K', 'A', 'C', 'F'}, optional
Specify the memory layout of the array. If object is not an array, the
newly created array will be in C order (row major) unless 'F' is
specified, in which case it will be in Fortran order (column major).
If object is an array the following holds.
===== ========= ===================================================
order no copy copy=True
===== ========= ===================================================
'K' unchanged F & C order preserved, otherwise most similar order
'A' unchanged F order if input is F and not C, otherwise C order
'C' C order C order
'F' F order F order
===== ========= ===================================================
When ``copy=False`` and a copy is made for other reasons, the result is
the same as if ``copy=True``, with some exceptions for `A`, see the
Notes section. The default order is 'K'.
subok : bool, optional
If True, then sub-classes will be passed-through, otherwise
the returned array will be forced to be a base-class array (default).
ndmin : int, optional
Specifies the minimum number of dimensions that the resulting
array should have. Ones will be pre-pended to the shape as
needed to meet this requirement.
Returns
-------
out : ndarray
An array object satisfying the specified requirements.
See Also
--------
empty, empty_like, zeros, zeros_like, ones, ones_like, full, full_like
Notes
-----
When order is 'A' and `object` is an array in neither 'C' nor 'F' order,
and a copy is forced by a change in dtype, then the order of the result is
not necessarily 'C' as expected. This is likely a bug.
Examples
--------
>>> np.array([1, 2, 3])
array([1, 2, 3])
Upcasting:
>>> np.array([1, 2, 3.0])
array([ 1., 2., 3.])
More than one dimension:
>>> np.array([[1, 2], [3, 4]])
array([[1, 2],
[3, 4]])
Minimum dimensions 2:
>>> np.array([1, 2, 3], ndmin=2)
array([[1, 2, 3]])
Type provided:
>>> np.array([1, 2, 3], dtype=complex)
array([ 1.+0.j, 2.+0.j, 3.+0.j])
Data-type consisting of more than one element:
>>> x = np.array([(1,2),(3,4)],dtype=[('a','<i4'),('b','<i4')])
>>> x['a']
array([1, 3])
Creating an array from sub-classes:
>>> np.array(np.mat('1 2; 3 4'))
array([[1, 2],
[3, 4]])
>>> np.array(np.mat('1 2; 3 4'), subok=True)
matrix([[1, 2],
[3, 4]])
Will cover more later, but first a quick intro to some other packages.
SciPy¶
Implements higher-level scientific algorithms using NumPy. Examples:
- Integration (scipy.integrate)
- Optimization (scipy.optimize)
- Interpolation (scipy.interpolate)
- Signal Processing (scipy.signal)
- Linear Algebra (scipy.linalg)
- Statistics (scipy.stats)
- File IO (scipy.io)
Also uses BLAS/LAPACK
import scipy
printcols(dir(scipy),2)
LowLevelCallable ndimage __numpy_version__ odr __version__ optimize cluster show_config fft signal fftpack sparse integrate spatial interpolate special io stats linalg test misc
printcols(dir(scipy.stats))
ConstantInputWarning bayes_mvs gausshyper matrix_normal rvs_ratio_uniforms DegenerateDataWarning bernoulli gaussian_kde maxwell scoreatpercentile FitError beta genexpon median_abs_deviation sem NearConstantInputWarning betabinom genextreme median_test semicircular NumericalInverseHermite betaprime gengamma mielke shapiro __all__ biasedurn genhalflogistic mode siegelslopes __builtins__ binned_statistic genhyperbolic moment sigmaclip __cached__ binned_statistic_2d geninvgauss monte_carlo_test skellam __doc__ binned_statistic_dd genlogistic mood skew __file__ binom gennorm morestats skewcauchy __loader__ binom_test genpareto moyal skewnorm __name__ binomtest geom mstats skewtest __package__ boltzmann gibrat mstats_basic somersd __path__ bootstrap gilbrat mstats_extras spearmanr __spec__ boschloo_exact gmean multinomial special_ortho_group _axis_nan_policy boxcox gompertz multiscale_graphcorr statlib _biasedurn boxcox_llf gstd multivariate_hypergeom stats _binned_statistic boxcox_normmax gumbel_l multivariate_normal studentized_range _binomtest boxcox_normplot gumbel_r multivariate_t t _boost bradford gzscore mvn test _common brunnermunzel halfcauchy mvsdist theilslopes _constants burr halfgennorm nakagami tiecorrect _continuous_distns burr12 halflogistic nbinom tmax _crosstab cauchy halfnorm ncf tmean _discrete_distns chi hmean nchypergeom_fisher tmin _distn_infrastructure chi2 hypergeom nchypergeom_wallenius trapezoid _distr_params chi2_contingency hypsecant nct trapz _entropy chisquare invgamma ncx2 triang _fit circmean invgauss nhypergeom trim1 _hypotests circstd invweibull norm trim_mean _hypotests_pythran circvar invwishart normaltest trimboth _kde combine_pvalues iqr norminvgauss truncexpon _ksstats contingency jarque_bera obrientransform truncnorm _levy_stable cosine johnsonsb ortho_group truncweibull_min _mannwhitneyu cramervonmises johnsonsu page_trend_test tsem _morestats cramervonmises_2samp kappa3 pareto tstd _mstats_basic crystalball kappa4 pearson3 ttest_1samp _mstats_extras cumfreq kde pearsonr ttest_ind _multivariate describe kendalltau percentileofscore ttest_ind_from_stats _mvn dgamma kruskal permutation_test ttest_rel _page_trend_test differential_entropy ks_1samp planck tukey_hsd _qmc dirichlet ks_2samp pmean tukeylambda _qmc_cy distributions ksone pointbiserialr tvar _relative_risk dlaplace kstat poisson uniform _resampling dweibull kstatvar power_divergence unitary_group _rvs_sampling energy_distance kstest powerlaw variation _sobol entropy kstwo powerlognorm vonmises _statlib epps_singleton_2samp kstwobign powernorm vonmises_line _stats erlang kurtosis ppcc_max wald _stats_mstats_common expon kurtosistest ppcc_plot wasserstein_distance _stats_py exponnorm laplace probplot weibull_max _tukeylambda_stats exponpow laplace_asymmetric qmc weibull_min _unuran exponweib levene randint weightedtau _variation f levy random_correlation wilcoxon _warnings_errors f_oneway levy_l rankdata wishart alexandergovern fatiguelife levy_stable ranksums wrapcauchy alpha find_repeats linregress rayleigh yeojohnson anderson fisher_exact loggamma rdist yeojohnson_llf anderson_ksamp fisk logistic recipinvgauss yeojohnson_normmax anglit fit loglaplace reciprocal yeojohnson_normplot ansari fligner lognorm relfreq yulesimon arcsine foldcauchy logser rice zipf argus foldnorm loguniform rv_continuous zipfian barnard_exact friedmanchisquare lomax rv_discrete zmap bartlett gamma mannwhitneyu rv_histogram zscore
Matplotlib¶
Tutorial from: https://github.com/amueller/scipy-2017-sklearn/blob/master/notebooks/02.Scientific_Computing_Tools_in_Python.ipynb
Another important part of machine learning is the visualization of data. The most common
tool for this in Python is matplotlib. It is an extremely flexible package, and
we will go over some basics here.
Jupyter has built-in "magic functions", the "matoplotlib inline" mode, which will draw the plots directly inside the notebook. Should be on by default.
%matplotlib inline
import matplotlib.pyplot as plt
# Plotting a line
x = np.linspace(0, 10, 100)
plt.plot(x, np.sin(x));
# Scatter-plot points
x = np.random.normal(size=500)
y = np.random.normal(size=500)
plt.scatter(x, y);
# Showing images using imshow
# - note that origin is at the top-left by default!
#x = np.linspace(1, 12, 100)
#y = x[:, np.newaxis]
#im = y * np.sin(x) * np.cos(y)
im = np.array([[1, 2, 3],[4,5,6],[6,7,8]])
import matplotlib.pyplot as plt
plt.imshow(im);
plt.colorbar();
plt.xlabel('x')
plt.ylabel('y')
plt.show();
# Contour plots
# - note that origin here is at the bottom-left by default!
plt.contour(im);
# 3D plotting
from mpl_toolkits.mplot3d import Axes3D
ax = plt.axes(projection='3d')
xgrid, ygrid = np.meshgrid(x, y.ravel())
ax.plot_surface(xgrid, ygrid, im, cmap=plt.cm.viridis, cstride=2, rstride=2, linewidth=0);
There are many more plot types available. See matplotlib gallery.
Test these examples: copy the Source Code
link, and put it in a notebook using the %load magic.
For example:
# %load http://matplotlib.org/mpl_examples/pylab_examples/ellipse_collection.py
SkLearn¶
Many Machine Learning functions.
Couple dozen core developers + hundreds of other contributors.
2011 tutorial has over 10,000 citations.
"Scikit-learn: Machine Learning in Python", Fabian Pedregosa, Gaël Varoquaux, Alexandre Gramfort, Vincent Michel, Bertrand Thirion, Olivier Grisel, Mathieu Blondel, Peter Prettenhofer, Ron Weiss, Vincent Dubourg, Jake Vanderplas, Alexandre Passos, David Cournapeau, Matthieu Brucher, Matthieu Perrot, Édouard Duchesnay; 12(Oct):2825−2830, 2011
Considered leading Machine Learning toolbox. Was getting discarded as field switched from sinlge CPU to multicore, but appears to be making comeback with parallel upgrades
# conda install anaconda::scikit-learn
import sklearn as sk
printcols(dir(sk),2)
__SKLEARN_SETUP__ base __all__ clone __builtins__ config_context __cached__ exceptions __check_build externals __doc__ get_config __file__ logger __loader__ logging __name__ os __package__ random __path__ set_config __spec__ setup_module __version__ show_versions _config sys _distributor_init utils
printcols(dir(sk.base),2)
BaseEstimator _check_feature_names_in BiclusterMixin _check_y ClassifierMixin _get_feature_names ClusterMixin _is_pairwise DensityMixin _num_features MetaEstimatorMixin _pprint MultiOutputMixin _safe_tags OutlierMixin check_X_y RegressorMixin check_array TransformerMixin clone _DEFAULT_TAGS copy _IS_32BIT defaultdict _OneToOneFeatureMixin estimator_html_repr _UnstableArchMixin get_config __builtins__ inspect __cached__ is_classifier __doc__ is_outlier_detector __file__ is_regressor __loader__ np __name__ platform __package__ re __spec__ warnings __version__
Machine Learning Framework using Sklearn¶
Given training data $(\mathbf x_{(i)},y_i)$ for $i=1,...,m$ --> lists of samples $\verb|X|$ and labels $\verb|y|$
Choose a model $f(\cdot)$ where we want to make $f(\mathbf x_{(i)})\approx y_i$ (for all $i$) --> choose sklearn estimator to use
Define a loss function $L(f(\mathbf x), y)$ to minimize by changing $f(\cdot)$ ...by adjusting the weights --> default choises for estimators, sometimes multiple options
The Sklearn API¶
sklearn has an Object Oriented interface
Most models/transforms/objects in sklearn are Estimator objects
class Estimator(object):
def fit(self, X, y=None):
"""Fit model to data X (and y)"""
self.some_attribute = self.some_fitting_method(X, y)
return self
def predict(self, X_test):
"""Make prediction based on passed features"""
pred = self.make_prediction(X_test)
return pred
model = Estimator()
The Estimator class defines a fit() method as well as a predict() method. For an instance of an Estimator stored in a variable model:
model.fit: fits the model with the passed in training data. For supervised models, it also accepts a second argumentythat corresponds to the labels (model.fit(X, y). For unsupervised models, there are no labels so you only need to pass in the feature matrix (model.fit(X))Since the interface is very OO, the instance itself stores the results of the
fitinternally. And as such you must alwaysfit()before youpredict()on the same object.model.predict: predicts new labels for any new datapoints passed in (model.predict(X_test)) and returns an array equal in length to the number of rows of what is passed in containing the predicted labels.
Types of subclass of estimator:¶
- Supervised
- Unsupervised
- Feature Processing
Supervised¶
Supervised estimators in addition to the above methods typically also have:
model.predict_proba: For classifiers that have a notion of probability (or some measure of confidence in a prediction) this method returns those "probabilities". The label with the highest probability is what is returned by themodel.predict()` mehod from above.model.score: For both classification and regression models, this method returns some measure of validation of the model (which is configurable). For example, in regression the default is typically R^2 and classification it is accuracy.
Unsupervised - Transformer interface¶
Some estimators in the library implement this.
Unsupervised in this case refers to any method that does not need labels, including unsupervised classifiers, preprocessing (like tf-idf), dimensionality reduction, etc.
The transformer interface usually defines two additional methods:
model.transform: Given an unsupervised model, transform the input into a new basis (or feature space). This accepts on argument (usually a feature matrix) and returns a matrix of the input transformed. Note: You need tofit()the model before you transform it.model.fit_transform: For some models you may not need tofit()andtransform()separately. In these cases it is more convenient to do both at the same time.
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(X, y)
print(neigh.predict([[1.1]]))
print(neigh.predict_proba([[0.9]]))
[0] [[0.66666667 0.33333333]]
Recap¶
- Mathematical software is implemented hierarchically
- BLAS = Lowest level(s), implemented on particular hardware, e.g. for SIMD processors
- Higher level functions (solvers and decompositions) calls BLAS to implement internal computations
- Structured and Sparse matrix libraries also call BLAS typically (convert large sparse problems to small dense problems)
- Modern alternatives also can utilize BLAS/LAPACK backend and also suppot hardware-specific replacements (e.g. CUDA)
IV. NumPy Basics¶
NumPy Arrays for Vectors¶
x = np.array([2,0,1,8])
x
array([2, 0, 1, 8])
NumPy arrays are zero-based like Python lists
print(x[0],x[3])
2 8
Matlab-ish slicing¶
A = np.array([[1,2,3],[4,5,6],[7,8,9]])
print(A)
[[1 2 3] [4 5 6] [7 8 9]]
print(A[:,0])
[1 4 7]
print(A[1,:])
[4 5 6]
print(A[1,1:])
[5 6]
$\verb|numpy.linalg|$¶
- Use BLAS and LAPACK to provide efficient low level implementations of standard linear algebra algorithms.
- Those libraries may be provided by NumPy itself using C versions of a subset of their reference implementations
- When possible, highly optimized libraries that take advantage of specialized processor functionality are preferred.
- Examples of such libraries are OpenBLAS, MKL (TM), and ATLAS.
https://docs.scipy.org/doc/numpy/reference/routines.linalg.html
Matrix and vector products¶
- dot(a, b[, out]) Dot product of two arrays.
- linalg.multi_dot(arrays) Compute the dot product of two or more arrays in a single function call, while automatically selecting the fastest evaluation order.
- vdot(a, b) Return the dot product of two vectors.
- inner(a, b) Inner product of two arrays.
- outer(a, b[, out]) Compute the outer product of two vectors.
- matmul(x1, x2, /[, out, casting, order, …]) Matrix product of two arrays.
- tensordot(a, b[, axes]) Compute tensor dot product along specified axes.
- einsum(subscripts, *operands[, out, dtype, …]) Evaluates the Einstein summation convention on the operands.
- einsum_path(subscripts, *operands[, optimize]) Evaluates the lowest cost contraction order for an einsum expression by considering the creation of intermediate arrays.
- linalg.matrix_power(a, n) Raise a square matrix to the (integer) power n.
- kron(a, b) Kronecker product of two arrays.
Decompositions¶
- linalg.cholesky(a) Cholesky decomposition.
- linalg.qr(a[, mode]) Compute the qr factorization of a matrix.
- linalg.svd(a[, full_matrices, compute_uv, …]) Singular Value Decomposition.
Matrix eigenvalues¶
- linalg.eig(a) Compute the eigenvalues and right eigenvectors of a square array.
- linalg.eigh(a[, UPLO]) Return the eigenvalues and eigenvectors of a complex Hermitian (conjugate symmetric) or a real symmetric matrix.
- linalg.eigvals(a) Compute the eigenvalues of a general matrix.
- linalg.eigvalsh(a[, UPLO]) Compute the eigenvalues of a complex Hermitian or real symmetric matrix.
Norms and other numbers¶
- linalg.norm(x[, ord, axis, keepdims]) Matrix or vector norm.
- linalg.cond(x[, p]) Compute the condition number of a matrix.
- linalg.det(a) Compute the determinant of an array.
- linalg.matrix_rank(M[, tol, hermitian]) Return matrix rank of array using SVD method
- linalg.slogdet(a) Compute the sign and (natural) logarithm of the determinant of an array.
- trace(a[, offset, axis1, axis2, dtype, out]) Return the sum along diagonals of the array.
Solving equations and inverting matrices¶
- linalg.solve(a, b) Solve a linear matrix equation, or system of linear scalar equations.
- linalg.tensorsolve(a, b[, axes]) Solve the tensor equation a x = b for x.
- linalg.lstsq(a, b[, rcond]) Return the least-squares solution to a linear matrix equation.
- linalg.inv(a) Compute the (multiplicative) inverse of a matrix.
- linalg.pinv(a[, rcond, hermitian]) Compute the (Moore-Penrose) pseudo-inverse of a matrix.
- linalg.tensorinv(a[, ind]) Compute the ‘inverse’ of an N-dimensional array.
"Vectorization"¶
Converting loops into linear algebra functions where loop is performed at lower level
E.g. instead of looping over a list to compute squares of elements, make into array and "square" array
v = [1,2,3,4,5]
v2 = []
for v_k in v:
v2.append(v_k**2)
v2
[1, 4, 9, 16, 25]
np.array(v)**2
array([ 1, 4, 9, 16, 25], dtype=int32)
Dot Product using NumPy¶
w = np.array([1, 2])
v = np.array([3, 4])
np.dot(w,v)
11
w = np.array([0, 1])
v = np.array([1, 0])
np.dot(w,v)
0
w = np.array([1, 2])
v = np.array([-2, 1])
np.dot(w,v)
0
Matrix-vector multiplication using NumPy - CAUTION¶
NumPy implements a broadcast version of multiplication when using the "*" operator.
It guesses what you mean rather by seeking ways the shapes match, rather than giving error.
w = np.array([[2,-6],[-1, 4]])
v = np.array([12,46])
w*v
array([[ 24, -276],
[ -12, 184]])
v+w
array([[14, 40],
[11, 50]])
"Broadcasting"¶
Multiply matrices or vectrors in an element-wise manner by repeating "singular" dimensions.
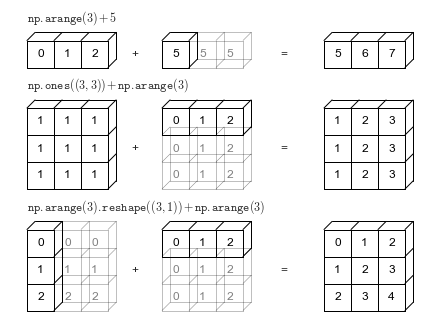
Matlab and Numpy automatically do this now.
Also (and previously) in matlab, e.g.: "brcm(@plus, A, x). numpy.broadcast
For true "Matrix-vector" multiplication, use matmul or "@"¶
a special case of matrix-matrix multiplication
w = np.array([[ 2, -6],
[-1, 4]])
v = np.array([[+1],
[-1]])
np.matmul(w,v)
array([[ 8],
[-5]])
w@v
array([ 8, -5])
Matrix-matrix multiplication¶
A = np.array([[1,2],[3, 4]])
B = np.array([[1,0],[1, 1]])
A*B
array([[1, 0],
[3, 4]])
What is this doing?¶
np.matmul(A,B)
array([[3, 2],
[7, 4]])
np.dot(A,B)
array([[3, 2],
[7, 4]])
A@B
array([[3, 2],
[7, 4]])
u = [1,2]
v = [1,3]
np.dot(np.array(u),np.array(v))
7
Reshaping vectors into matrices and whatever else you want¶
x = np.array([1,2,3,4])
x = x.reshape(4,1)
print(x.reshape(4,1))
[[1] [2] [3] [4]]
print(x.reshape(2,2))
[[1 2] [3 4]]
print(x)
x_T = x.transpose()
print (x_T)
print (x_T.shape)
print(x.T)
[[1] [2] [3] [4]] [[1 2 3 4]] (1, 4) [[1 2 3 4]]
Famous matrices in NumPy¶
np.zeros((3,4))
array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
np.ones((3,4))
array([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
np.eye(3)
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
D = np.diag([1,2,3])
print(D)
[[1 0 0] [0 2 0] [0 0 3]]
np.diag(D)
array([1, 2, 3])
np.random.rand(3,4) # note two inputs, not tuple
array([[0.99147344, 0.01075122, 0.81974321, 0.10942128],
[0.94041317, 0.50408574, 0.71896232, 0.12113072],
[0.77483078, 0.32627551, 0.44489225, 0.13208849]])
np.random.randn(3,4)
array([[ 1.09642959, 1.40715723, -0.30932909, 0.66846735],
[ 0.22536484, -0.08283707, -0.60713286, -0.16836462],
[-1.20191307, 1.53390883, -0.48587343, -0.84379159]])
NumPy Inverse¶
A = np.array([[1,2],[4,5]])
iA = np.linalg.inv(A)
print(iA)
print(np.matmul(A,iA))
[[-1.66666667 0.66666667] [ 1.33333333 -0.33333333]] [[1. 0.] [0. 1.]]
2.*8.
16.0
A = np.random.randint(0, 10, size=(3, 3))
A_inv = np.linalg.inv(A)
print(A)
print(A_inv)
print(np.matmul(A,A_inv))
[[2 6 4] [5 7 1] [5 3 2]] [[-1.25000000e-01 -1.11022302e-17 2.50000000e-01] [ 5.68181818e-02 1.81818182e-01 -2.04545455e-01] [ 2.27272727e-01 -2.72727273e-01 1.81818182e-01]] [[ 1.00000000e+00 0.00000000e+00 -1.11022302e-16] [-2.77555756e-17 1.00000000e+00 -8.32667268e-17] [-5.55111512e-17 0.00000000e+00 1.00000000e+00]]
Note that "hard zeros" rarely exist in real world due to limited numerical precision.
Eigenvalue Decomposition in NumPy¶
A = np.asarray([[.3,.1,.6],[.1,.3,.6],[.15,.15,.70]])
np.linalg.eig(A)
(array([1. , 0.2, 0.1]),
array([[-5.77350269e-01, -7.07106781e-01, -6.66666667e-01],
[-5.77350269e-01, 7.07106781e-01, -6.66666667e-01],
[-5.77350269e-01, -2.74027523e-16, 3.33333333e-01]]))
Note there's only one return
(u,s) = np.linalg.eig(A)
print(u)
print(s)
[1. 0.2 0.1] [[-5.77350269e-01 -7.07106781e-01 -6.66666667e-01] [-5.77350269e-01 7.07106781e-01 -6.66666667e-01] [-5.77350269e-01 -2.74027523e-16 3.33333333e-01]]
help(np.linalg.eig)
Help on function eig in module numpy.linalg.linalg:
eig(a)
Compute the eigenvalues and right eigenvectors of a square array.
Parameters
----------
a : (..., M, M) array
Matrices for which the eigenvalues and right eigenvectors will
be computed
Returns
-------
w : (..., M) array
The eigenvalues, each repeated according to its multiplicity.
The eigenvalues are not necessarily ordered. The resulting
array will be of complex type, unless the imaginary part is
zero in which case it will be cast to a real type. When `a`
is real the resulting eigenvalues will be real (0 imaginary
part) or occur in conjugate pairs
v : (..., M, M) array
The normalized (unit "length") eigenvectors, such that the
column ``v[:,i]`` is the eigenvector corresponding to the
eigenvalue ``w[i]``.
Raises
------
LinAlgError
If the eigenvalue computation does not converge.
See Also
--------
eigvals : eigenvalues of a non-symmetric array.
eigh : eigenvalues and eigenvectors of a symmetric or Hermitian
(conjugate symmetric) array.
eigvalsh : eigenvalues of a symmetric or Hermitian (conjugate symmetric)
array.
Notes
-----
.. versionadded:: 1.8.0
Broadcasting rules apply, see the `numpy.linalg` documentation for
details.
This is implemented using the _geev LAPACK routines which compute
the eigenvalues and eigenvectors of general square arrays.
The number `w` is an eigenvalue of `a` if there exists a vector
`v` such that ``dot(a,v) = w * v``. Thus, the arrays `a`, `w`, and
`v` satisfy the equations ``dot(a[:,:], v[:,i]) = w[i] * v[:,i]``
for :math:`i \in \{0,...,M-1\}`.
The array `v` of eigenvectors may not be of maximum rank, that is, some
of the columns may be linearly dependent, although round-off error may
obscure that fact. If the eigenvalues are all different, then theoretically
the eigenvectors are linearly independent. Likewise, the (complex-valued)
matrix of eigenvectors `v` is unitary if the matrix `a` is normal, i.e.,
if ``dot(a, a.H) = dot(a.H, a)``, where `a.H` denotes the conjugate
transpose of `a`.
Finally, it is emphasized that `v` consists of the *right* (as in
right-hand side) eigenvectors of `a`. A vector `y` satisfying
``dot(y.T, a) = z * y.T`` for some number `z` is called a *left*
eigenvector of `a`, and, in general, the left and right eigenvectors
of a matrix are not necessarily the (perhaps conjugate) transposes
of each other.
References
----------
G. Strang, *Linear Algebra and Its Applications*, 2nd Ed., Orlando, FL,
Academic Press, Inc., 1980, Various pp.
Examples
--------
>>> from numpy import linalg as LA
(Almost) trivial example with real e-values and e-vectors.
>>> w, v = LA.eig(np.diag((1, 2, 3)))
>>> w; v
array([ 1., 2., 3.])
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
Real matrix possessing complex e-values and e-vectors; note that the
e-values are complex conjugates of each other.
>>> w, v = LA.eig(np.array([[1, -1], [1, 1]]))
>>> w; v
array([ 1. + 1.j, 1. - 1.j])
array([[ 0.70710678+0.j , 0.70710678+0.j ],
[ 0.00000000-0.70710678j, 0.00000000+0.70710678j]])
Complex-valued matrix with real e-values (but complex-valued e-vectors);
note that a.conj().T = a, i.e., a is Hermitian.
>>> a = np.array([[1, 1j], [-1j, 1]])
>>> w, v = LA.eig(a)
>>> w; v
array([ 2.00000000e+00+0.j, 5.98651912e-36+0.j]) # i.e., {2, 0}
array([[ 0.00000000+0.70710678j, 0.70710678+0.j ],
[ 0.70710678+0.j , 0.00000000+0.70710678j]])
Be careful about round-off error!
>>> a = np.array([[1 + 1e-9, 0], [0, 1 - 1e-9]])
>>> # Theor. e-values are 1 +/- 1e-9
>>> w, v = LA.eig(a)
>>> w; v
array([ 1., 1.])
array([[ 1., 0.],
[ 0., 1.]])
SVD in NumPy¶
np.linalg.svd(A)
(array([[-0.32453643, -0.9458732 ],
[-0.9458732 , 0.32453643]]),
array([6.76782894, 0.44327362]),
array([[-0.60699365, -0.79470668],
[ 0.79470668, -0.60699365]]))
Note outputs are U, S, and V-transposed
help(np.linalg.svd)
Help on function svd in module numpy.linalg.linalg:
svd(a, full_matrices=True, compute_uv=True)
Singular Value Decomposition.
When `a` is a 2D array, it is factorized as ``u @ np.diag(s) @ vh
= (u * s) @ vh``, where `u` and `vh` are 2D unitary arrays and `s` is a 1D
array of `a`'s singular values. When `a` is higher-dimensional, SVD is
applied in stacked mode as explained below.
Parameters
----------
a : (..., M, N) array_like
A real or complex array with ``a.ndim >= 2``.
full_matrices : bool, optional
If True (default), `u` and `vh` have the shapes ``(..., M, M)`` and
``(..., N, N)``, respectively. Otherwise, the shapes are
``(..., M, K)`` and ``(..., K, N)``, respectively, where
``K = min(M, N)``.
compute_uv : bool, optional
Whether or not to compute `u` and `vh` in addition to `s`. True
by default.
Returns
-------
u : { (..., M, M), (..., M, K) } array
Unitary array(s). The first ``a.ndim - 2`` dimensions have the same
size as those of the input `a`. The size of the last two dimensions
depends on the value of `full_matrices`. Only returned when
`compute_uv` is True.
s : (..., K) array
Vector(s) with the singular values, within each vector sorted in
descending order. The first ``a.ndim - 2`` dimensions have the same
size as those of the input `a`.
vh : { (..., N, N), (..., K, N) } array
Unitary array(s). The first ``a.ndim - 2`` dimensions have the same
size as those of the input `a`. The size of the last two dimensions
depends on the value of `full_matrices`. Only returned when
`compute_uv` is True.
Raises
------
LinAlgError
If SVD computation does not converge.
Notes
-----
.. versionchanged:: 1.8.0
Broadcasting rules apply, see the `numpy.linalg` documentation for
details.
The decomposition is performed using LAPACK routine ``_gesdd``.
SVD is usually described for the factorization of a 2D matrix :math:`A`.
The higher-dimensional case will be discussed below. In the 2D case, SVD is
written as :math:`A = U S V^H`, where :math:`A = a`, :math:`U= u`,
:math:`S= \mathtt{np.diag}(s)` and :math:`V^H = vh`. The 1D array `s`
contains the singular values of `a` and `u` and `vh` are unitary. The rows
of `vh` are the eigenvectors of :math:`A^H A` and the columns of `u` are
the eigenvectors of :math:`A A^H`. In both cases the corresponding
(possibly non-zero) eigenvalues are given by ``s**2``.
If `a` has more than two dimensions, then broadcasting rules apply, as
explained in :ref:`routines.linalg-broadcasting`. This means that SVD is
working in "stacked" mode: it iterates over all indices of the first
``a.ndim - 2`` dimensions and for each combination SVD is applied to the
last two indices. The matrix `a` can be reconstructed from the
decomposition with either ``(u * s[..., None, :]) @ vh`` or
``u @ (s[..., None] * vh)``. (The ``@`` operator can be replaced by the
function ``np.matmul`` for python versions below 3.5.)
If `a` is a ``matrix`` object (as opposed to an ``ndarray``), then so are
all the return values.
Examples
--------
>>> a = np.random.randn(9, 6) + 1j*np.random.randn(9, 6)
>>> b = np.random.randn(2, 7, 8, 3) + 1j*np.random.randn(2, 7, 8, 3)
Reconstruction based on full SVD, 2D case:
>>> u, s, vh = np.linalg.svd(a, full_matrices=True)
>>> u.shape, s.shape, vh.shape
((9, 9), (6,), (6, 6))
>>> np.allclose(a, np.dot(u[:, :6] * s, vh))
True
>>> smat = np.zeros((9, 6), dtype=complex)
>>> smat[:6, :6] = np.diag(s)
>>> np.allclose(a, np.dot(u, np.dot(smat, vh)))
True
Reconstruction based on reduced SVD, 2D case:
>>> u, s, vh = np.linalg.svd(a, full_matrices=False)
>>> u.shape, s.shape, vh.shape
((9, 6), (6,), (6, 6))
>>> np.allclose(a, np.dot(u * s, vh))
True
>>> smat = np.diag(s)
>>> np.allclose(a, np.dot(u, np.dot(smat, vh)))
True
Reconstruction based on full SVD, 4D case:
>>> u, s, vh = np.linalg.svd(b, full_matrices=True)
>>> u.shape, s.shape, vh.shape
((2, 7, 8, 8), (2, 7, 3), (2, 7, 3, 3))
>>> np.allclose(b, np.matmul(u[..., :3] * s[..., None, :], vh))
True
>>> np.allclose(b, np.matmul(u[..., :3], s[..., None] * vh))
True
Reconstruction based on reduced SVD, 4D case:
>>> u, s, vh = np.linalg.svd(b, full_matrices=False)
>>> u.shape, s.shape, vh.shape
((2, 7, 8, 3), (2, 7, 3), (2, 7, 3, 3))
>>> np.allclose(b, np.matmul(u * s[..., None, :], vh))
True
>>> np.allclose(b, np.matmul(u, s[..., None] * vh))
True
QR in NumPy¶
Q,R = np.linalg.qr(A)
print(Q)
#print(R)
[[-0.85714286 0.39439831 -0.33129458] [-0.28571429 -0.89922814 -0.33129458] [-0.42857143 -0.18931119 0.88345221]]
np.dot(Q[:,2],Q[:,2])
1.0
Q.T@Q
array([[ 1.00000000e+00, 3.25682983e-17, -6.47535828e-17],
[ 3.25682983e-17, 1.00000000e+00, 1.03449228e-16],
[-6.47535828e-17, 1.03449228e-16, 1.00000000e+00]])
help(np.linalg.qr)
Help on function qr in module numpy.linalg.linalg:
qr(a, mode='reduced')
Compute the qr factorization of a matrix.
Factor the matrix `a` as *qr*, where `q` is orthonormal and `r` is
upper-triangular.
Parameters
----------
a : array_like, shape (M, N)
Matrix to be factored.
mode : {'reduced', 'complete', 'r', 'raw', 'full', 'economic'}, optional
If K = min(M, N), then
* 'reduced' : returns q, r with dimensions (M, K), (K, N) (default)
* 'complete' : returns q, r with dimensions (M, M), (M, N)
* 'r' : returns r only with dimensions (K, N)
* 'raw' : returns h, tau with dimensions (N, M), (K,)
* 'full' : alias of 'reduced', deprecated
* 'economic' : returns h from 'raw', deprecated.
The options 'reduced', 'complete, and 'raw' are new in numpy 1.8,
see the notes for more information. The default is 'reduced', and to
maintain backward compatibility with earlier versions of numpy both
it and the old default 'full' can be omitted. Note that array h
returned in 'raw' mode is transposed for calling Fortran. The
'economic' mode is deprecated. The modes 'full' and 'economic' may
be passed using only the first letter for backwards compatibility,
but all others must be spelled out. See the Notes for more
explanation.
Returns
-------
q : ndarray of float or complex, optional
A matrix with orthonormal columns. When mode = 'complete' the
result is an orthogonal/unitary matrix depending on whether or not
a is real/complex. The determinant may be either +/- 1 in that
case.
r : ndarray of float or complex, optional
The upper-triangular matrix.
(h, tau) : ndarrays of np.double or np.cdouble, optional
The array h contains the Householder reflectors that generate q
along with r. The tau array contains scaling factors for the
reflectors. In the deprecated 'economic' mode only h is returned.
Raises
------
LinAlgError
If factoring fails.
Notes
-----
This is an interface to the LAPACK routines dgeqrf, zgeqrf,
dorgqr, and zungqr.
For more information on the qr factorization, see for example:
http://en.wikipedia.org/wiki/QR_factorization
Subclasses of `ndarray` are preserved except for the 'raw' mode. So if
`a` is of type `matrix`, all the return values will be matrices too.
New 'reduced', 'complete', and 'raw' options for mode were added in
NumPy 1.8.0 and the old option 'full' was made an alias of 'reduced'. In
addition the options 'full' and 'economic' were deprecated. Because
'full' was the previous default and 'reduced' is the new default,
backward compatibility can be maintained by letting `mode` default.
The 'raw' option was added so that LAPACK routines that can multiply
arrays by q using the Householder reflectors can be used. Note that in
this case the returned arrays are of type np.double or np.cdouble and
the h array is transposed to be FORTRAN compatible. No routines using
the 'raw' return are currently exposed by numpy, but some are available
in lapack_lite and just await the necessary work.
Examples
--------
>>> a = np.random.randn(9, 6)
>>> q, r = np.linalg.qr(a)
>>> np.allclose(a, np.dot(q, r)) # a does equal qr
True
>>> r2 = np.linalg.qr(a, mode='r')
>>> r3 = np.linalg.qr(a, mode='economic')
>>> np.allclose(r, r2) # mode='r' returns the same r as mode='full'
True
>>> # But only triu parts are guaranteed equal when mode='economic'
>>> np.allclose(r, np.triu(r3[:6,:6], k=0))
True
Example illustrating a common use of `qr`: solving of least squares
problems
What are the least-squares-best `m` and `y0` in ``y = y0 + mx`` for
the following data: {(0,1), (1,0), (1,2), (2,1)}. (Graph the points
and you'll see that it should be y0 = 0, m = 1.) The answer is provided
by solving the over-determined matrix equation ``Ax = b``, where::
A = array([[0, 1], [1, 1], [1, 1], [2, 1]])
x = array([[y0], [m]])
b = array([[1], [0], [2], [1]])
If A = qr such that q is orthonormal (which is always possible via
Gram-Schmidt), then ``x = inv(r) * (q.T) * b``. (In numpy practice,
however, we simply use `lstsq`.)
>>> A = np.array([[0, 1], [1, 1], [1, 1], [2, 1]])
>>> A
array([[0, 1],
[1, 1],
[1, 1],
[2, 1]])
>>> b = np.array([1, 0, 2, 1])
>>> q, r = LA.qr(A)
>>> p = np.dot(q.T, b)
>>> np.dot(LA.inv(r), p)
array([ 1.1e-16, 1.0e+00])
Lab: Least-squares regression various ways¶
Load Boston house prices dataset.
Formulate linear system and try using inverse and pseudoinverse to solve.
from sklearn.datasets import load_boston
boston = load_boston()
print(dir(boston))
print(boston.data.shape)
print(boston.feature_names)
print(boston.DESCR)
['DESCR', 'data', 'feature_names', 'filename', 'target']
(506, 13)
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
'B' 'LSTAT']
.. _boston_dataset:
Boston house prices dataset
---------------------------
**Data Set Characteristics:**
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10,000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000's
:Missing Attribute Values: None
:Creator: Harrison, D. and Rubinfeld, D.L.
This is a copy of UCI ML housing dataset.
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980. N.B. Various transformations are used in the table on
pages 244-261 of the latter.
The Boston house-price data has been used in many machine learning papers that address regression
problems.
.. topic:: References
- Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
- Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
Nonlinear regression¶
(easy way) - Linear regression after nonlinear transformation
Old: \begin{align} \mathbf y = \beta_0 + \beta_1 \mathbf x_{(1)} + \beta_2 \mathbf x_{(2)} +...+ \beta_n \mathbf x_{(n)} + \varepsilon , \; \; \; \mathbf x_{(i)} = \begin{bmatrix} x_{(i),1} \\x_{(i),2} \\ \vdots \\ x_{(i),m} \end{bmatrix} \end{align}
New: \begin{align} \mathbf y = \beta_0 + \beta_1 \mathbf x'_{(1)} + \beta_2 \mathbf x'_{(2)} +...+ \beta_n \mathbf x'_{(n)} + \varepsilon, \;\;\; \mathbf x'_{(i)} = \begin{bmatrix} f_{(i)}(x_1) \\f_{(i)}(x_2) \\ \vdots \\ f_{(i)}(x_m) \end{bmatrix} \end{align}
...Feature Engineering
Polynomial regression - simple powers of data¶
New model: $\mathbf y = \beta_0 + \beta_1 \mathbf x'_{(1)} + \beta_2 \mathbf x'_{(2)} +...+ \beta_n \mathbf x'_{(n)} + \varepsilon$
$$\mathbf x'_{(i)} = \begin{bmatrix} f_{(i)}(x_1) \\f_{(i)}(x_2) \\ \vdots \\ f_{(i)}(x_m) \end{bmatrix} = \begin{bmatrix} x_{1}^i \\x_{2}^i \\ \vdots \\ x_{m}^i \end{bmatrix}$$
Exercise: write the model equations out for 3D case, i.e. $\bf x$ is just $x_1$, $x_2$, and $x_3$.
Polynomial regression¶
show_polyfit_ho_example_results(dosage,conc_noisy,(1,2,3,4,5,6));
order: 1, residual: 56.6204627002199 order: 2, residual: 43.28483436298878 order: 3, residual: 38.90189854595423 order: 4, residual: 21.166171682768383 order: 5, residual: 13.416800916508517 order: 6, residual: 1.8203750586044797e-11