BDS 761: Data Science and Machine Learning I

Topic 4: Precision and Norms
This topic:¶
- Numerical precision (on modern desktop computers)
- Norms, distances, and basic stats
- k-means clustering
Readings:
- Intro to Applied Linear Algebra Ch. 3 & 4 https://web.stanford.edu/~boyd/vmls/
Numerical Precision¶
Binary numbers¶
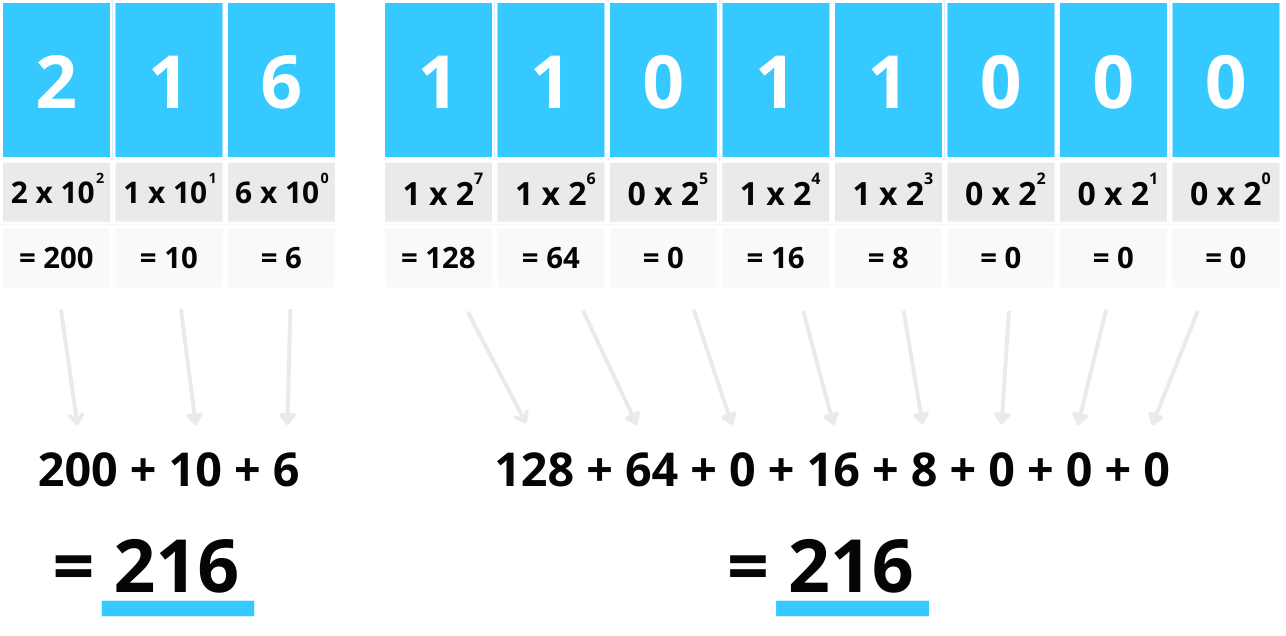
https://mikkegoes.com/computer-science-binary-code-explained/
The basis for all modern computing.
What set of numbers can be represented with the above binary scheme and 8 bits?
What is the largest number possible with 8 bits? with 32 bits?
How many decimal digits do these amount to roughly?
bin(216) # gives binary representation of integer
'0b11011000'
import numpy as np
np.base_repr(216, base=2, padding=0)
'11011000'
Hexadecimal¶
Base-16 system. Effectively groups four binary digits into each hex digit.
for k in range(0,32):
print(f'{k:4d} {bin(k):>8s} {hex(k):>5s}.')
0 0b0 0x0. 1 0b1 0x1. 2 0b10 0x2. 3 0b11 0x3. 4 0b100 0x4. 5 0b101 0x5. 6 0b110 0x6. 7 0b111 0x7. 8 0b1000 0x8. 9 0b1001 0x9. 10 0b1010 0xa. 11 0b1011 0xb. 12 0b1100 0xc. 13 0b1101 0xd. 14 0b1110 0xe. 15 0b1111 0xf. 16 0b10000 0x10. 17 0b10001 0x11. 18 0b10010 0x12. 19 0b10011 0x13. 20 0b10100 0x14. 21 0b10101 0x15. 22 0b10110 0x16. 23 0b10111 0x17. 24 0b11000 0x18. 25 0b11001 0x19. 26 0b11010 0x1a. 27 0b11011 0x1b. 28 0b11100 0x1c. 29 0b11101 0x1d. 30 0b11110 0x1e. 31 0b11111 0x1f.
Floating point numbers¶
IEEE 754 standard for representing a real number with a 32-bit (or 64-bit) word.

$$x = (-1)^{\text{sign}} \times \text{fraction} \times 2^\text{exponent}$$
Similar approach to achieve higher precision using 64-bit words
Note that two version of zero are possible, +0 and -0, depending on sign bit
$\pm$ Infinity = exponents all 1's, fraction all 0's
Not-a-number (NaN) = exponents all 1's, fraction not all 0's.
https://learn.microsoft.com/en-us/cpp/build/ieee-floating-point-representation?view=msvc-170
1./0.
--------------------------------------------------------------------------- ZeroDivisionError Traceback (most recent call last) ~\AppData\Local\Temp\ipykernel_26264\832528835.py in <module> ----> 1 1./0. ZeroDivisionError: float division by zero
import numpy as np
1/np.array([0.]), -1./np.array([0.])
C:\Users\micro\AppData\Local\Temp\ipykernel_26264\3923875365.py:3: RuntimeWarning: divide by zero encountered in true_divide 1/np.array([0.]), -1./np.array([0.])
(array([inf]), array([-inf]))
0.0/0.0
--------------------------------------------------------------------------- ZeroDivisionError Traceback (most recent call last) ~\AppData\Local\Temp\ipykernel_26264\1949058463.py in <module> ----> 1 0.0/0.0 ZeroDivisionError: float division by zero
0.0/np.array([0.0])
C:\Users\micro\AppData\Local\Temp\ipykernel_26264\844779733.py:1: RuntimeWarning: invalid value encountered in true_divide 0.0/np.array([0.0])
array([nan])
0*np.nan
nan
np.inf*np.nan
nan
Commonly used number types¶
| Common names | bits |
|---|---|
| character (char) | 8 |
| integers (int) | 32 |
| unsigned integers (uint) | 32 |
| floating-pointing numbers (float, single) | 32,64 |
| double precision floating point numbers (double) | 64 |
| short integers (short) | 16 |
| long integers (long) | 32 |
| double long integers (longlong) | 64 |
| unsigned long integers (ulong) | 64 |
Note that number of bits used vary depending on hardware, compiler, ...
Precision (a.k.a. number of bits) is often added to the type name, e.g. float32.
Working with limited precision¶
Number of decimal digits from the number of binary exponent bits
- 32 bit floats have about 7 digits of precision
- 64 bit floats have about 16 digits precision
Must keep in mind that decimal numbers are always approximate.
1 + 1e-12
1.000000000001
1 + 1e-25
1.0
1 + 1e-25 == 1
True
1 + 1e-12 == 1
False
1e-25 + 1e-12
1.0000000000001e-12
A = np.random.randint(0, 10, size=(3, 3))
A_inv = np.linalg.inv(A)
print(A@A_inv) # matrix times its inverse should be identity
[[ 1.00000000e+00 0.00000000e+00 -2.22044605e-16] [-3.70074342e-18 1.00000000e+00 5.55111512e-17] [ 0.00000000e+00 0.00000000e+00 1.00000000e+00]]
Floating-Point Arithmetic¶
Floating point computations are not exact
$$ a+b \approx c$$Result will be nearest floating point number that can be represented with the binary system used.
hard zeros ~ special case when "0.0" really is all zeros (for fractional part) in binary
Logic, however, is still exact
0.1 + 0.1 + 0.1 == 0.3
False
0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 == 1.0
False
round(0.1 + 0.1 + 0.1, 5) == round(0.3, 5) # round to 5 digits precision
True
import math
math.isclose(0.1 + 0.1 + 0.1, 0.3)
True
# but some calculations can still work
a=3
b=a/3
c=b*3
c==a
True
so what's the lesson here?
Overflow and Underflow¶
Overflow = not enough bits to represent number (number too big, positive or negative)
Underflow = not enough precision to represent number (number too small)
# Integer Overflow (int8)
import numpy as np
a = np.int8(120)
b = np.int8(10)
overflow_result = a + b
print("a =", a)
print("b =", b)
print("a + b =", overflow_result) # Wraps around to a negative number
print("Expected (120 + 10) = 130, but stored as int8:", np.int8(130))
a = 120 b = 10 a + b = -126 Expected (120 + 10) = 130, but stored as int8: -126
C:\Users\micro\AppData\Local\Temp\ipykernel_11188\1159094512.py:7: RuntimeWarning: overflow encountered in byte_scalars overflow_result = a + b
# Integer Overflow (int16)
a16 = np.int16(32760)
b16 = np.int16(10)
print("a16 + b16 =", a16 + b16) # Correct
print("int16 max =", np.iinfo(np.int16).max)
# Show overflow explicitly
overflow16 = np.int16(np.iinfo(np.int16).max + 1)
print("Overflow: int16(max + 1) =", overflow16)
a16 + b16 = -32766 int16 max = 32767 Overflow: int16(max + 1) = -32768
C:\Users\micro\AppData\Local\Temp\ipykernel_11188\934376104.py:5: RuntimeWarning: overflow encountered in short_scalars
print("a16 + b16 =", a16 + b16) # Correct
# Negative Integer "Overflow" (int8)
x = np.int8(-120)
y = np.int8(-10)
overflow_result = x + y
print("x =", x)
print("y =", y)
print("x + y =", overflow_result) # Wraps around to a positive number
print("Expected (-120 - 10) = -130, but stored as int8:", np.int8(-130))
x = -120 y = -10 x + y = 126 Expected (-120 - 10) = -130, but stored as int8: 126
C:\Users\micro\AppData\Local\Temp\ipykernel_11188\1048983399.py:5: RuntimeWarning: overflow encountered in byte_scalars overflow_result = x + y
# Floating-Point Overflow
# This will overflow for float32 but not for float64
import numpy as np
a = np.float32(1e38)
b = np.float32(10)
overflow_result = a * b
print("a =", a)
print("b =", b)
print("a * b =", overflow_result) # Will be inf
print("Is inf?", np.isinf(overflow_result))
a = 1e+38 b = 10.0 a * b = inf Is inf? True
C:\Users\micro\AppData\Local\Temp\ipykernel_11188\591289397.py:8: RuntimeWarning: overflow encountered in float_scalars overflow_result = a * b
# Floating-Point Underflow
x = np.float32(1e-38)
y = np.float32(1e-10)
underflow_result = x * y
print("x =", x)
print("y =", y)
print("x * y =", underflow_result) # Will be 0.0
print("Is zero?", underflow_result == 0.0)
x = 1e-38 y = 1e-10 x * y = 0.0 Is zero? True
# Float64 Example
a64 = np.float64(1e308)
b64 = np.float64(10)
print("a64 * b64 =", a64 * b64) # Will overflow
--- Float64 Safe Example --- a64 * b64 = inf
C:\Users\micro\AppData\Local\Temp\ipykernel_11188\1189525556.py:5: RuntimeWarning: overflow encountered in double_scalars
print("a64 * b64 =", a64 * b64) # Will overflow
x64 = np.float64(1e-308)
y64 = np.float64(1e-10)
print("x64 * y64 =", x64 * y64) # Will underflow?
x64 * y64 = 1e-318
Preventing Overflow¶
Use larger number for result
import numpy as np
print("\n--- Preventing Overflow with Type Promotion ---")
# Start with int8
a = np.int8(120)
b = np.int8(10)
# Promote to int16 before addition
safe_result = np.int16(a) + np.int16(b)
print("a (int8) =", a)
print("b (int8) =", b)
print("a + b with int8 =", np.int8(a + b)) # Overflows
print("a + b with int16 =", safe_result) # Correct result 130
--- Preventing Overflow with Type Promotion --- a (int8) = 120 b (int8) = 10 a + b with int8 = -126 a + b with int16 = 130
C:\Users\micro\AppData\Local\Temp\ipykernel_11188\3938648987.py:12: RuntimeWarning: overflow encountered in byte_scalars
print("a + b with int8 =", np.int8(a + b)) # Overflows
Precision Errors in Matrix Multiplication¶
Trade off precision for speed and memory use
import numpy as np
import time
# Matrix size
N = 1000 # Adjust based on system memory/performance
# Generate base float64 matrices from uniform [0, 255]
A64 = (np.random.rand(N, N) * 255).astype(np.float64)
B64 = (np.random.rand(N, N) * 255).astype(np.float64)
print("\n--- float64 ---")
size_bytes = A64.nbytes + B64.nbytes
print(f"Matrix size: {size_bytes / 1e6:.2f} MB")
start_time = time.time()
C64 = A64 @ B64
end_time = time.time()
print(f"Time taken: {end_time - start_time:.4f} seconds")
print("\n--- float32 ---")
A32 = A64.astype(np.float32)
B32 = B64.astype(np.float32)
size_bytes = A32.nbytes + B32.nbytes
print(f"Matrix size: {size_bytes / 1e6:.2f} MB")
start_time = time.time()
C32 = A32 @ B32
end_time = time.time()
print(f"Time taken: {end_time - start_time:.4f} seconds")
print("\n--- float16 ---")
A16 = A64.astype(np.float16)
B16 = B64.astype(np.float16)
size_bytes = A16.nbytes + B16.nbytes
print(f"Matrix size: {size_bytes / 1e6:.2f} MB")
start_time = time.time()
C16 = A16 @ B16
end_time = time.time()
print(f"Time taken: {end_time - start_time:.4f} seconds")
print("\n--- int32 ---")
Aint32 = A64.astype(np.int32)
Bint32 = B64.astype(np.int32)
size_bytes = Aint32.nbytes + Bint32.nbytes
print(f"Matrix size: {size_bytes / 1e6:.2f} MB")
start_time = time.time()
Cint32 = Aint32 @ Bint32
end_time = time.time()
print(f"Time taken: {end_time - start_time:.4f} seconds")
print("\n--- int64 ---")
Aint64 = A64.astype(np.int64)
Bint64 = B64.astype(np.int64)
size_bytes = Aint64.nbytes + Bint64.nbytes
print(f"Matrix size: {size_bytes / 1e6:.2f} MB")
start_time = time.time()
Cint64 = Aint64 @ Bint64
end_time = time.time()
print(f"Time taken: {end_time - start_time:.4f} seconds")
# Upsample results to float64 for fair comparison
C16_up = C16.astype(np.float64)
C32_up = C32.astype(np.float64)
Cint32_up = Cint32.astype(np.float64)
Cint64_up = Cint64.astype(np.float64)
# Compute maximum absolute differences
print("\n--- Maximum Absolute Differences ---")
print(f"max|C64 - C32| = {np.max(np.abs(C64 - C32_up)):.6e}")
print(f"max|C64 - C16| = {np.max(np.abs(C64 - C16_up)):.6e}")
print(f"max|C32 - C16| = {np.max(np.abs(C32_up - C16_up)):.6e}")
print(f"max|C64 - int32| = {np.max(np.abs(C64 - Cint32_up)):.6e}")
print(f"max|C64 - int64| = {np.max(np.abs(C64 - Cint64_up)):.6e}")
--- float64 --- Matrix size: 16.00 MB Time taken: 0.0224 seconds --- float32 --- Matrix size: 8.00 MB Time taken: 0.0077 seconds --- float16 --- Matrix size: 4.00 MB
C:\Users\keith\AppData\Local\Temp\ipykernel_12860\449388697.py:35: RuntimeWarning: overflow encountered in matmul C16 = A16 @ B16
Time taken: 7.8111 seconds --- int32 --- Matrix size: 8.00 MB Time taken: 2.1030 seconds --- int64 --- Matrix size: 16.00 MB Time taken: 2.6975 seconds --- Maximum Absolute Differences --- max|C64 - C32| = 7.997219e+00 max|C64 - C16| = inf max|C32 - C16| = inf max|C64 - int32| = 1.394282e+05 max|C64 - int64| = 1.394282e+05
import numpy as np
import time
# Matrix size
N = 1000 # Adjust based on system memory/performance
# Generate base float64 matrices from uniform [0, 255]
A64 = (np.random.rand(N, N) * 255).astype(np.float64)
B64 = (np.random.rand(N, N) * 255).astype(np.float64)
print("\n--- float64 ---")
size_bytes = A64.nbytes + B64.nbytes
print(f"Matrix size: {size_bytes / 1e6:.2f} MB")
start_time = time.time()
C64 = A64 @ B64
end_time = time.time()
print(f"Time taken: {end_time - start_time:.4f} seconds")
print("\n--- float32 ---")
A32 = A64.astype(np.float32)
B32 = B64.astype(np.float32)
size_bytes = A32.nbytes + B32.nbytes
print(f"Matrix size: {size_bytes / 1e6:.2f} MB")
start_time = time.time()
C32 = A32 @ B32
end_time = time.time()
print(f"Time taken: {end_time - start_time:.4f} seconds")
print("\n--- float16 ---")
A16 = A64.astype(np.float16)
B16 = B64.astype(np.float16)
size_bytes = A16.nbytes + B16.nbytes
print(f"Matrix size: {size_bytes / 1e6:.2f} MB")
start_time = time.time()
C16 = A16 @ B16
end_time = time.time()
print(f"Time taken: {end_time - start_time:.4f} seconds")
print("\n--- int32 ---")
Aint32 = A64.astype(np.int32)
Bint32 = B64.astype(np.int32)
size_bytes = Aint32.nbytes + Bint32.nbytes
print(f"Matrix size: {size_bytes / 1e6:.2f} MB")
start_time = time.time()
Cint32 = Aint32 @ Bint32
end_time = time.time()
print(f"Time taken: {end_time - start_time:.4f} seconds")
print("\n--- int64 ---")
Aint64 = A64.astype(np.int64)
Bint64 = B64.astype(np.int64)
size_bytes = Aint64.nbytes + Bint64.nbytes
print(f"Matrix size: {size_bytes / 1e6:.2f} MB")
start_time = time.time()
Cint64 = Aint64 @ Bint64
end_time = time.time()
print(f"Time taken: {end_time - start_time:.4f} seconds")
# Upsample results to float64 for fair comparison
C16_up = C16.astype(np.float64)
C32_up = C32.astype(np.float64)
Cint32_up = Cint32.astype(np.float64)
Cint64_up = Cint64.astype(np.float64)
# Compute maximum absolute differences
print("\n--- Maximum Absolute Differences ---")
print(f"max|C64 - C32| = {np.max(np.abs(C64 - C32_up)):.6e}")
print(f"max|C64 - C16| = {np.max(np.abs(C64 - C16_up)):.6e}")
print(f"max|C32 - C16| = {np.max(np.abs(C32_up - C16_up)):.6e}")
print(f"max|C64 - int32| = {np.max(np.abs(C64 - Cint32_up)):.6e}")
print(f"max|C64 - int64| = {np.max(np.abs(C64 - Cint64_up)):.6e}")
--- float64 --- Matrix size: 16.00 MB Time taken: 0.1867 seconds --- float32 --- Matrix size: 8.00 MB Time taken: 0.0340 seconds --- float16 --- Matrix size: 4.00 MB
C:\Users\micro\AppData\Local\Temp\ipykernel_11188\449388697.py:35: RuntimeWarning: overflow encountered in matmul C16 = A16 @ B16
Time taken: 6.0759 seconds --- int32 --- Matrix size: 8.00 MB Time taken: 2.8536 seconds --- int64 --- Matrix size: 16.00 MB Time taken: 3.8560 seconds --- Maximum Absolute Differences --- max|C64 - C32| = 1.330282e+01 max|C64 - C16| = inf max|C32 - C16| = inf max|C64 - int32| = 1.374838e+05 max|C64 - int64| = 1.374838e+05
Norms & Distances¶
Metric¶
Basically, boil multiple numbers (vectors, matrices, time series,...) or entire functions down to a single number
Examples
- GDP of economy
- BMI (body-mass index)
- A statistic (mean, variance, ...)
- Vector norms...
Always can be critized as discarding important info, but need to use something
Euclidean Norm¶
$$ \|x\| = \sqrt{x_1^2+x_2^2+\dotsb+x_n^2} $$"Length" of a vector (as opposed to length of the data structure, i.e. number of dimensions)
Also known as $\|x\|_2$, the "two-norm"
Example¶
$$\left\Vert \begin{pmatrix}2 \\ -1\\2 \end{pmatrix}\right\Vert = ?$$Also use a built-in function to do this
Exercise: give Euclidean norm using dot products
Root-mean-square value (RMS)¶
$$ rms(x) = \sqrt{\frac{x_1^2+x_2^2+\dotsb+x_n^2}{n}} = \frac{1}{\sqrt{n}}\|x\| $$root(mean(square(x)))
Exercise: give Euclidean norm of sum of vectors $x+y$ in terms of dot products
(use result of previous exercise and work only with vectors)
$$||x+y||_2 = \text{dot}(?,?) + \text{dot}(?,?) + ???$$$$ \sqrt{(x_1+y_1)(x_1+y_1) + (x_2+y_2)(x_2+y_2) + ... } = $$Chebychev Inequality¶
If $x$ is a length-$n$ vector with $k$ entries satisfying $|x_i|\ge a$ for some constant $a>0$, then
$$\frac{k}{n} \le \left( \frac{rms(x)}{a}\right)^2$$Basically tells how much elements can deviate from the rms
Derive by noting that $\Vert x\Vert^2 \ge ka^2$
Motivation for other types of norms¶
Consider the list of data for different "dimensions", for one person, product, etc.
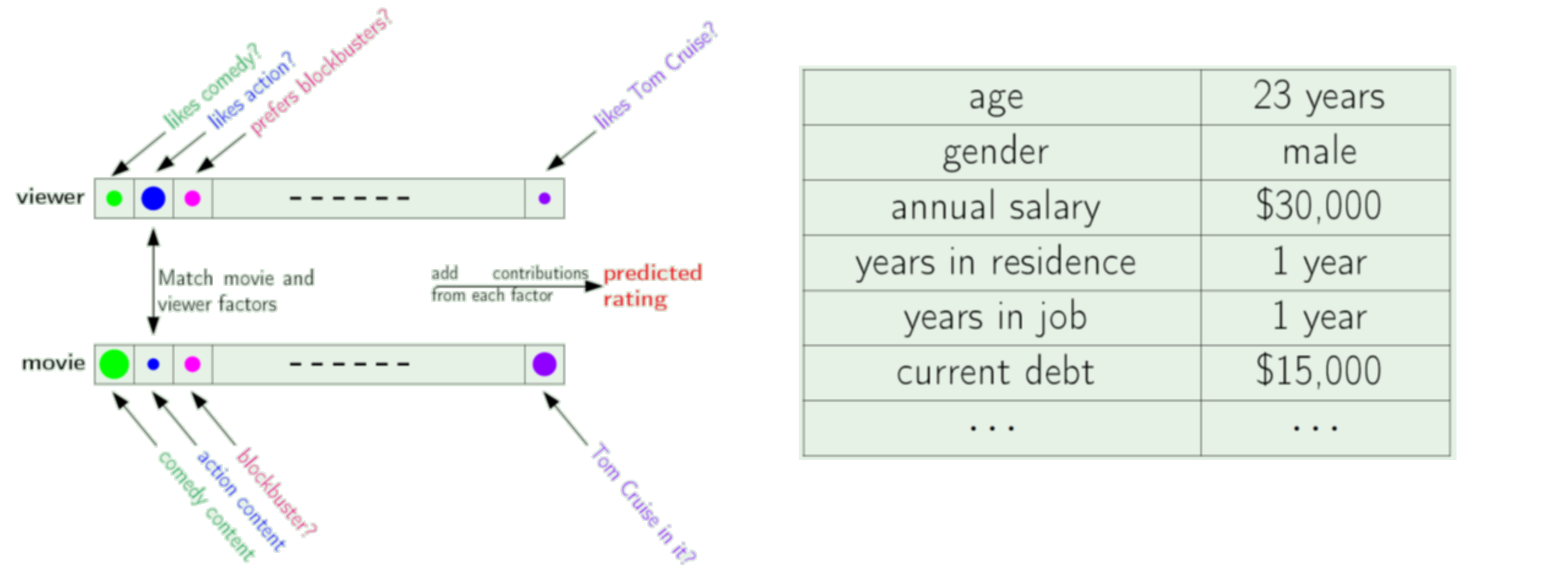
Does it make sense to compute Euclidean distance to tell us how "big" the vector is?
Norms¶
A norm is a vector "length". Often denoted generally as $\Vert \mathbf x \Vert$.
Properties
- Non-negativity: $\Vert \mathbf x \Vert \geq 0$
- Zero upon equality: $\Vert \mathbf x \Vert = 0 \iff \mathbf x = \mathbf 0$
- Absolute scalability: $\Vert \alpha \mathbf x \Vert = |\alpha| \Vert \mathbf x \Vert$ for scalar $\alpha$
- Triangle Inequality: $\Vert \mathbf x + \mathbf z\Vert \leq \Vert \mathbf x\Vert + \Vert \mathbf z\Vert$
$p$-Norms¶
For any $n$-dimensional real or complex vector. i.e. $x \in \mathbb{R}^n \text{ or } \mathbb{C}^n$
$$ \|x\|_p = \left(|x_1|^p+|x_2|^p+\dotsb+|x_n|^p\right)^{\frac{1}{p}} $$$$ \|x\|_p = \begin{pmatrix}\sum_{i=1}^n{|x_i|^p} \end{pmatrix}^{\frac{1}{p}} $$Consider the norms we have looked at. What is $p$?
Famous "norms"¶
- $\ell_2$ norm
- $\ell_1$ norm
- $\ell_\infty$ norm
- $\ell_p$ norm
- "$\ell_0$" norm
Note we often lazily write these as e.g. "L2" norm
Exercise: Wite out the $p$-norms for a vector $x$ for $p$ = 1,2,0,$\infty$... $ \|x\|_p = \begin{pmatrix}\sum_{i=1}^n{|x_i|^p} \end{pmatrix}^{\frac{1}{p}} $
Exercise: test the conditions for each
import numpy as np
v = [1,3,1,4]
for p in range(1,10):
print(p,np.power(sum(np.power(np.abs(np.array(v)),p)),1/p))
1 9.0 2 5.196152422706632 3 4.530654896083492 4 4.290915128445443 5 4.175344598847825 6 4.110988070009078 7 4.0723049678331895 8 4.048006070825583 9 4.032310478684122
Exercise¶
What are the norms of $\vec{a} = \begin{bmatrix}1\\3\\1\\-4\end{bmatrix}$ and $\vec{b} = \begin{bmatrix}2\\0\\1\\-2\end{bmatrix}$?
"Norm balls"¶
The Set $\{x | \Vert x \Vert_p \le 1 \}$, $ \|x\|_p = \begin{pmatrix}\sum_{i=1}^n{|x_i|^p} \end{pmatrix}^{\frac{1}{p}} $
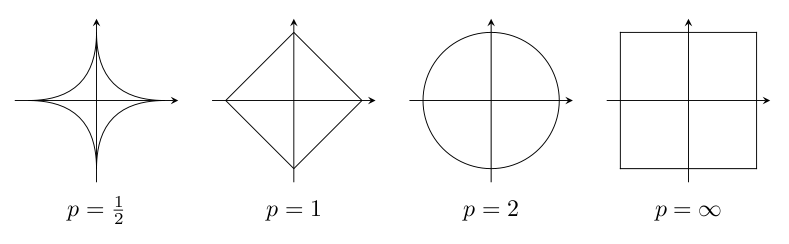
Note how $\Vert x \Vert_a \le \Vert x \Vert_b$ if $a\ge b$
Norms, Inner products, and angles¶
Inner product = length squared
$$v \cdot v = v^T v = \| v \|_2^2 = \| v \|_2\| v \|_2$$Angle $\theta$ between two vectors
$$v \cdot w = v^T w = \| v \|_2\| w \|_2 \cos\theta$$Cauchy-Schwartz Inequality $v^T w \le \| v \|\| w \|$¶
Triangle Inequality¶
$$\| v + w \| \le \| v \|+\| w \|$$Derive by noting that $\| v + w \|^2 = \|v\|^2 + v^Tw + \|w\|^2$ then use Cauchy-Schwartz and complete square
$S$-norm¶
For any symmetric positive definite matrix $S$
$$\| v \|_S^2 = v^T S v$$$S$ inner product¶
$$<v,w>_S = v^T S w$$Minkowski metric¶
Proposed by Lorentz for 4-dimensional spacetime, $v = (x,y,z,t)^T$, $c$ is speed of light
$$\| v\|^2_M = x^2+y^2+z^2-ct^2$$Is it a true norm?
II. Distances¶
Euclidean distance between two vectors $a$ and $b$ in $\mathbb{R}^{n}$:¶
$$d(\mathbf a,\mathbf b) = \sqrt{\sum_{i=1}^{n}(b_i-a_i)^2} = \Vert \mathbf b - \mathbf a \Vert_2$$Again this may not make sense for various vectors. Many alternatives...
Norm versus Distance¶
What is the relationship?
Distance properties¶
A distance metic $d(\mathbf x,\mathbf y)$ must satisfy four particular conditions to be considered a metric:
- Non-negativity: $d(\mathbf x,\mathbf y) \geq 0$
- Zero upon equality: $d(\mathbf x,\mathbf y) = 0 \iff \mathbf x = \mathbf y$
- Commutativity of arguments: $d(\mathbf x,\mathbf y) = d(\mathbf y,\mathbf x)$
- Triangle Inequality: $d(\mathbf x,\mathbf z) \leq d(\mathbf x,\mathbf y) + d(\mathbf y,\mathbf z)$
Exercise¶
Write the Euclidean distance between two points entirely in terms of dot products.
What does this tell you about using dot products to compare vector similarity?
Triangle Inequality¶
$\Vert \mathbf x + \mathbf z\Vert \leq \Vert \mathbf x\Vert + \Vert \mathbf z\Vert$
$d(\mathbf a,\mathbf c) \leq d(\mathbf a,\mathbf b) + d(\mathbf b,\mathbf c)$
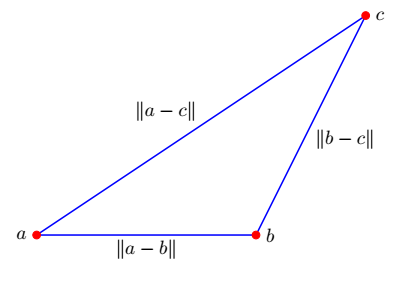
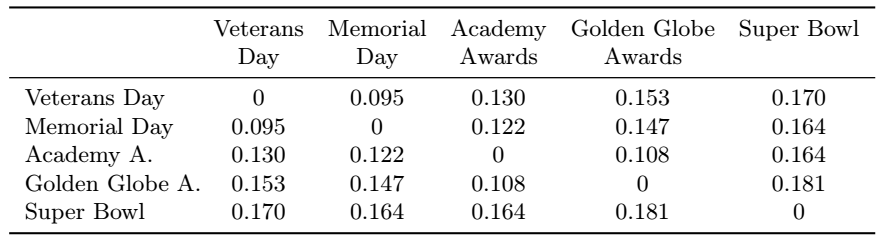
Application: feature distances¶
Recommender syatem based on most similar customers to movie properties

Question: what are the units of the distance here?
Application: rms prediction error¶
Time series prediction (stocks or temperature) compared to truth in retrospect
Manhattan or "Taxicab" Distance, also "Rectilinear distance"¶
Measures the relationships between points at right angles, meaning that we sum the absolute value of the difference in vector coordinates.
This metric is sensitive to rotation.
$$d_{M}(a,b) = \sum_{i=1}^{n}|b_i-a_i|$$Exercise¶
Does it fulfill the 4 conditions?
- Non-negativity: $d(\mathbf x,\mathbf y) \geq 0$
- Zero upon equality: $d(\mathbf x,\mathbf y) = 0 \iff \mathbf x = \mathbf y$
- Commutativity of arguments: $d(\mathbf x,\mathbf y) = d(\mathbf y,\mathbf x)$
- Triangle Inequality: $d(\mathbf x,\mathbf z) \leq d(\mathbf x,\mathbf y) + d(\mathbf y,\mathbf z)$
Chebyschev Distance¶
The Chebyschev distance or sometimes the $L^{\infty}$ metric, between two vectors is simply the the greatest of their differences along any coordinate dimension:
$$d_{\infty}(\mathbf a,\mathbf b) = \max_{i}{|(b_i-a_i)|}$$...consider
- Non-negativity: $d(\mathbf x,\mathbf y) \geq 0$
- Zero upon equality: $d(\mathbf x,\mathbf y) = 0 \iff \mathbf x = \mathbf y$
- Commutativity of arguments: $d(\mathbf x,\mathbf y) = d(\mathbf y,\mathbf x)$
- Triangle Inequality: $d(\mathbf x,\mathbf z) \leq d(\mathbf x,\mathbf y) + d(\mathbf y,\mathbf z)$
Cosine Distance¶
High school geometry: $\mathbf a \cdot \mathbf b = \|\mathbf a\|_2\|\mathbf b\|_2 \cos\theta$
Only depends on angle between the vectors
$$d_{\cos}(\mathbf a,\mathbf b) = 1-\frac{\mathbf a \cdot \mathbf b}{\|\mathbf a\|\|\mathbf b\|} = 1 - \cos\theta$$...consider (extra carefully)
- Non-negativity: $d(\mathbf x,\mathbf y) \geq 0$
- Zero upon equality: $d(\mathbf x,\mathbf y) = 0 \iff \mathbf x = \mathbf y$
- Commutativity of arguments: $d(\mathbf x,\mathbf y) = d(\mathbf y,\mathbf x)$
- Triangle Inequality: $d(\mathbf x,\mathbf z) \leq d(\mathbf x,\mathbf y) + d(\mathbf y,\mathbf z)$
Exercise¶
Implement the metrics manually and compute distances between:
$ \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix}$ and $ \begin{bmatrix} 5 \\ 6 \\ 7 \\ 8 \end{bmatrix}$
IV. Statistics with Python¶
Random sampling¶
- rand() - uniform random numbers in [0,1]
- randn() - standard normal random numbers (zero mean, unit variance)
from numpy import random
printcols(dir(random))
BitGenerator __package__ default_rng noncentral_chisquare set_state Generator __path__ dirichlet noncentral_f shuffle MT19937 __spec__ exponential normal standard_cauchy PCG64 _bounded_integers f pareto standard_exponential PCG64DXSM _common gamma permutation standard_gamma Philox _generator geometric poisson standard_normal RandomState _mt19937 get_state power standard_t SFC64 _pcg64 gumbel rand test SeedSequence _philox hypergeometric randint triangular __RandomState_ctor _pickle laplace randn uniform __all__ _sfc64 logistic random vonmises __builtins__ beta lognormal random_integers wald __cached__ binomial logseries random_sample weibull __doc__ bit_generator mtrand ranf zipf __file__ bytes multinomial rayleigh __loader__ chisquare multivariate_normal sample __name__ choice negative_binomial seed
The Normal Distribution¶
- Also known as Gaussian distribution
import numpy as np
from matplotlib import pyplot as plt
def univariate_normal(x, mean, var):
return ((1. / np.sqrt(2 * np.pi * var)) * np.exp(-(x - mean)**2 / (2 * var)))
x = np.linspace(-5,5,1000)
plt.plot(x,univariate_normal(x,1,2));
plt.show()
Exercise¶
Generate normal random samples with mean of 1 and variance of 1
Plot histogram versus the theoretical distribution
Try different numbers of samples
Statistics¶
Consider the relation between norms and simple statistical quantities
\begin{align} \text{Population mean} &= \mu = \frac{\sum_{i=1}^N x_i}{N} \\ \text{Sample mean} &= \bar{x} = \frac{\sum_{i=1}^n x_i}{n} \\ \text{Population variance} &= \sigma^2 = \frac{\sum_{i=1}^N (x_i - \mu)^2}{N} \\ \text{Sample variance} &= s^2 = \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n - 1} = \frac{\sum_{i=1}^n x_i^2 - \frac{1}{n}(\sum_{i=1}^n x_i)^2}{n - 1} \\ \text{Standard deviation} &= \sqrt{\text{Variance}} \end{align}Exercise¶
Load a dataset from sklearn and compute mean and variance of a column
Standardize the column
Now compute mean and variance of the result
The Standard Normal Distribution $Z$¶
- If $X$ is a normal r.v. with $E(X) = \mu$ and $V(X) = \sigma^2$
- $Z$ is a normal r.v. with $E(X) = 0$ and $V(X) = 1$
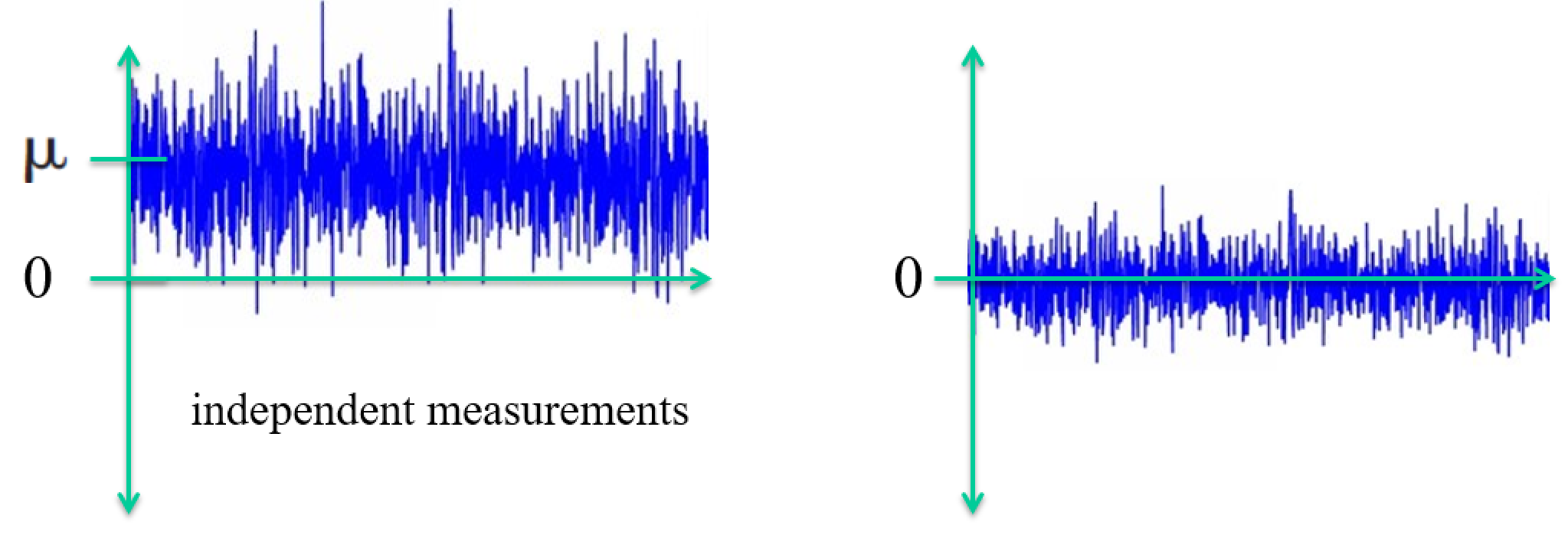
Standardizing data has two tasks¶
$$ Z = \frac{X-\mu}{\sigma} $$- Remove the mean
- scale by the standard deviation
Lab: Standardizing data¶
Standardize the columns of the Iris dataset using linear algebra.
Test it worked by computing the mean and norm of each column.
Multivariate Gaussian (for $n$ dimensions)¶
$$ f(\mathbf x) = \frac{1}{ \sqrt{2 \pi^n |\boldsymbol\Sigma|}} \exp \left(- \frac{1}{2} (\mathbf x - \boldsymbol \mu)^T \boldsymbol\Sigma^{-1} (\mathbf x - \boldsymbol \mu) \right) \text{, for } \mathbf x \in R^n $$- Mean vector as centroid of distribution
- Covariance matrix describes spread - correlations between variables $\Sigma_{ij} = S_{\mathbf x_i \mathbf x_j}$
def multivariate_normal(x, n, mean, cov):
return (1./(np.sqrt((2*np.pi)**n * np.linalg.det(cov))) * np.exp(-1/2*(x - mean).T@np.linalg.inv(cov)@(x - mean)))
mean = np.array([35,70])
cov = 100*np.array([[1,.5],[.5,1]])
pic = np.zeros((100,100))
for x1 in np.arange(0,100):
for x2 in np.arange(0,100):
x = [x1,x2]
pic[x1,x2] = multivariate_normal(x, 2, mean, cov)
plt.contour(pic);
Tricky Exercise¶
Consider a $m \times 3$ matrix $\mathbf A$ with columns $\mathbf x, \mathbf y$, and $\mathbf z$ (each a vector of data).
How would you efficiently standardize the three columns to make $\bar{\mathbf A}$.
What are the elements of $\bar{\mathbf A}^T \bar{\mathbf A}$?
Exercise:¶
Assume you have a vector containing samples. Write the following in terms of norms and dot products:
- mean
- variance
- Correlation coefficient
- Covariance
So what does this tell you about comparing things using distances versus dot products versus statistics?
V. Clustering¶
Dimensionality Reduction¶
Describing data with less information
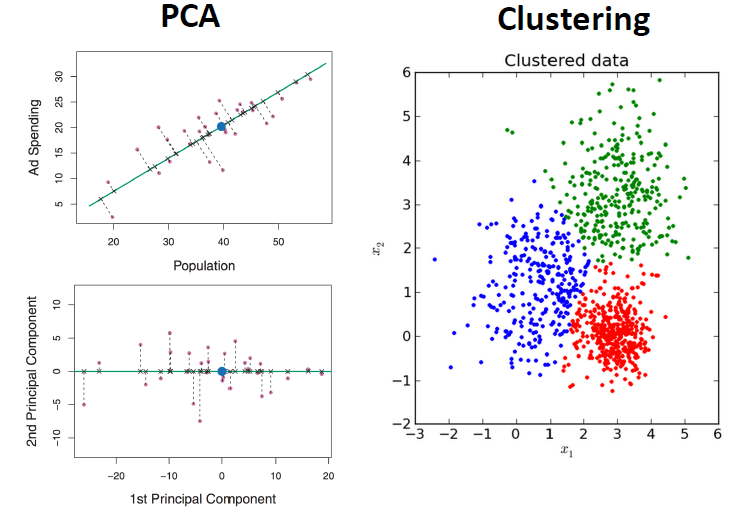
How are PCA and Clustering leading to less information? Consider a dataset.
What are the benefits?
Clustering References¶
https://en.wikipedia.org/wiki/K-means_clustering
https://en.wikipedia.org/wiki/K-means%2B%2B - kmeans++
https://www.youtube.com/watch?v=IuRb3y8qKX4 - video with visualization of training progress
https://www.youtube.com/watch?v=cWSnFaSjgBU - more on visualization
http://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html
Marketing Motivation¶
You want to make a certain number of products for a large population of customers. We know a number of features describing each of the customers, and are able to target a product to a certain customer profile.
E.g.: different customers prefer cars which are fast, or get good gas mileage, or are cheap, or are luxurious and presigious (i.e., expensive), or are big, or are little, etc. And in various combinations.
The customers vary widely so we wish to make k products which cover as closely as possible what as many as possible customers would like.
The better you can do this, the better your products will sell.
K-means clustering¶
- K clusters, centers are the means of cluster members.
- Each sample belongs to the cluster who's mean is nearest.
- Iteratively recompute membership and means (greedy optimization)
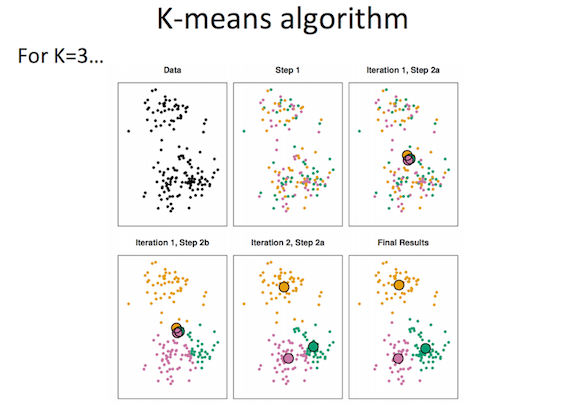
K-means algorithm¶
- Assign a number from 1 to K to each of N data points randomly
- While cluster assignments keep changing:
- For each of K clusters:
- Calculate cluster centroid
- For each of N points:
- Assign point to centroid it is closest to
- For each of K clusters:
Consider the possible ways to vary details in this method? How many clusters? How calculate distance?
k-Means as Greedy Optimization¶
The sum of all distances between members of a cluster gives a total length (a squared length can be viewed as a measure of "energy").
Within-Cluster-Variation: $WCV(C_k) = \dfrac{1}{|C_k|}\sum_{i, j \in C_k}d(x_{i}-x_{j})$, where $d(x_{i}-x_{j})$ is a distance metric of your choice.
k-means tries to minimize the net lengths over all clusters.
If you plotted this for each iteration, what would the plot look like?
Lab¶
Implement k-means clustering algorithm using scikit on IRIS, MNIST datasets.
Compute the net WCV for various options.
Look at result and WCV with different initializations.
Try varying the metric used in the clustering.
Vary k and plot WCV versus k.