BDS 761: Data Science and Machine Learning I

Topic 7: Graph and Network Methods
I. Introduction to Graphs¶
Motivation¶
Graphs & Networks are used to describe relationship structures.
Example: Social network - a description of the relationships between people
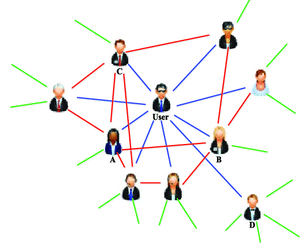
Disease factor causation?¶
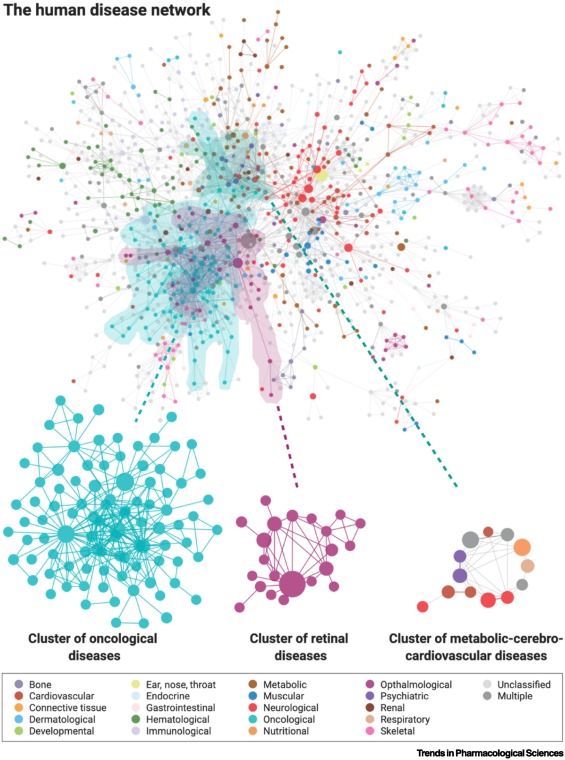
Nogales, Cristian, et al. "Network pharmacology: curing causal mechanisms instead of treating symptoms." Trends in pharmacological sciences 43.2 (2022): 136-150.
Brain activity¶
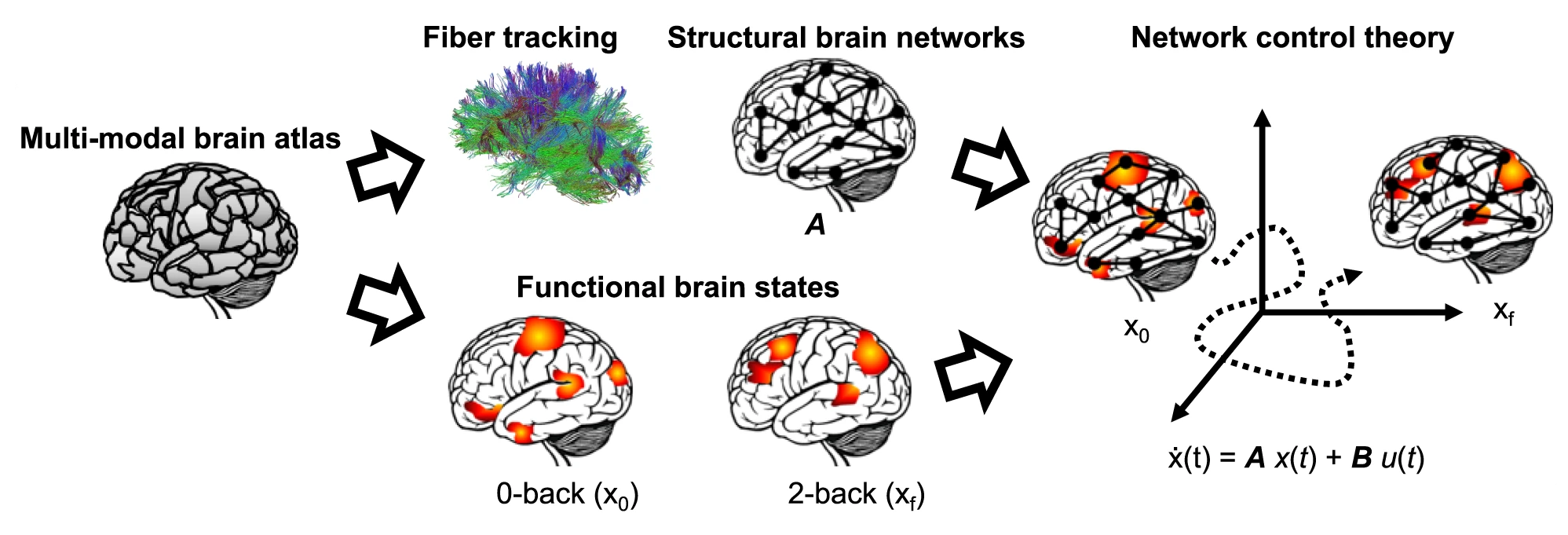
Braun, Urs, et al. "Brain network dynamics during working memory are modulated by dopamine and diminished in schizophrenia." Nature communications 12.1 (2021): 3478.
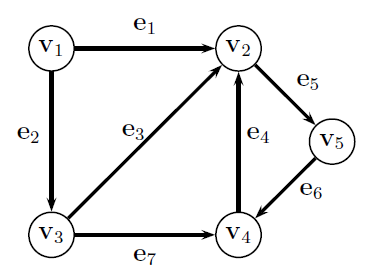
Graph Definition¶
$$G = (V,E)$$
- A set of Nodes $V=\{v_1, ..., v_n\}$
- A set of Edges $E = \{e_1, ..., e_m\}, e_i \in V\times V $ - either binary (there or not there) or weighted, between pairs of nodes
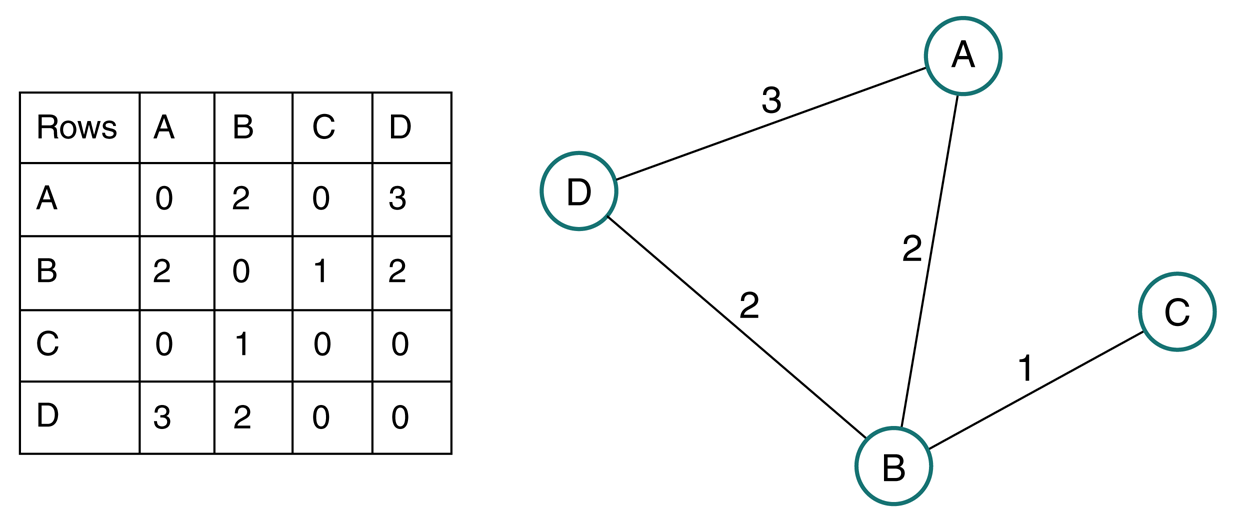
Adjacency Matrix¶
an $n\times n$ matrix $\mathbf A$ where...
- $A_{i,j}=+1$ if there is an edge from nodes $i$ to $j$
- $A_{j,i}=+1$ if there is an edge from nodes $j$ to $i$

$$\mathbf A = \begin{bmatrix} 0 & 1 & 1 & 0 & 0\\ 1 & 0 & 1 & 1 & 1\\ 1 & 1 & 0 & 1 & 0\\ 0 & 1 & 1 & 0 & 1\\ 0 & 1 & 0 & 1 & 0 \end{bmatrix} $$
Adjacency matrix interpretation¶
Diffusion operator - applying $\mathbf A$ to vector of values at nodes results in values at neighboring nodes.
Eigenvector intuition - consider what it means, therefore, if $\mathbf A \mathbf x = \lambda \mathbf x$
Work through a simple example.
Degree¶
Node Degree - $d(v_i)$ number of edges entering or leaving node $v_i$ = In_degree + out_degree
Degree Matrix - diagonal matrix of node degrees
$$\mathbf D = \begin{bmatrix} d_{1} & 0 & 0 & 0 & 0\\ 0 & d_{2} & 0 & 0 & 0\\ 0 & 0 & d_{3} & 0 & 0\\ 0 & 0 & 0 & d_{4} & 0\\ 0 & 0 & 0 & 0 & d_{5} \end{bmatrix} = \begin{bmatrix} 2 & 0 & 0 & 0 & 0\\ 0 & 4 & 0 & 0 & 0\\ 0 & 0 & 3 & 0 & 0\\ 0 & 0 & 0 & 3 & 0\\ 0 & 0 & 0 & 0 & 2 \end{bmatrix} $$
Consider how to compute this from adjacency matrix
Adjacency Matrix - Variants¶
- Signed
- Directed
- Weighted (often called $\mathbf W$)
Consider what each can be used to represent.
Also can have any combination of these properties.
Network methods overwhelmingly focus on unsigned, undirected, binary case. Weighted version also common.
Weighted graph¶
Generally define weight matrix $\mathbf W$ as weighted analog to adjacency matrix, since also can define a binary adjacency matrix for same graph.
Degree of node in weighted graph is sum of weights of edges connecting node
Degree vector $\mathbf d = \mathbf W \mathbf 1$
Degree matrix $\mathbf D = \text{diag}(\mathbf d)$
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
from networkx import from_numpy_array
# generate random adjacency matrix
A = np.random.rand(5,5)
#A = (A>0.5).astype(int) # make integer edges
A = A*(A>0.7) # make real edges
print(A)
G = from_numpy_array(A, create_using=nx.DiGraph)
layout = nx.spring_layout(G)
nx.draw(G, layout)
#nx.draw_networkx_edge_labels(G, pos=layout)
#nx.draw_networkx_labels(G, pos=layout);
[[0. 0. 0.89422099 0.79640697 0. ] [0.98087499 0. 0. 0.78447931 0. ] [0. 0. 0.96194397 0. 0.72479588] [0.99169098 0. 0. 0. 0. ] [0. 0. 0. 0. 0.86987698]]
Creating Networks from data¶
For a set of variables $\{x_1, ..., x_m\}$
We have a vector of samples of each of the random variables $\{\mathbf x_1, ..., \mathbf x_m\}$
We also like to create a matrix of data $\mathbf X$ from the vectors, where rows are samples and columns are features
Defining edges
- truncated distance: if $\Vert \mathbf x_i - \mathbf x_j\Vert < d_{c}$, $e_{ij}=1$, else $e_{ij}=0$
- similarity: $$\exp\left( -\frac{1}{2\sigma^2}\Vert \mathbf x_i - \mathbf x_j\Vert^2\right)$$
- statistical measures?
from sklearn import datasets
dir(datasets)
['__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__path__', '__spec__', '_base', '_california_housing', '_covtype', '_kddcup99', '_lfw', '_olivetti_faces', '_openml', '_rcv1', '_samples_generator', '_species_distributions', '_svmlight_format_fast', '_svmlight_format_io', '_twenty_newsgroups', 'clear_data_home', 'dump_svmlight_file', 'fetch_20newsgroups', 'fetch_20newsgroups_vectorized', 'fetch_california_housing', 'fetch_covtype', 'fetch_kddcup99', 'fetch_lfw_pairs', 'fetch_lfw_people', 'fetch_olivetti_faces', 'fetch_openml', 'fetch_rcv1', 'fetch_species_distributions', 'get_data_home', 'load_boston', 'load_breast_cancer', 'load_diabetes', 'load_digits', 'load_files', 'load_iris', 'load_linnerud', 'load_sample_image', 'load_sample_images', 'load_svmlight_file', 'load_svmlight_files', 'load_wine', 'make_biclusters', 'make_blobs', 'make_checkerboard', 'make_circles', 'make_classification', 'make_friedman1', 'make_friedman2', 'make_friedman3', 'make_gaussian_quantiles', 'make_hastie_10_2', 'make_low_rank_matrix', 'make_moons', 'make_multilabel_classification', 'make_regression', 'make_s_curve', 'make_sparse_coded_signal', 'make_sparse_spd_matrix', 'make_sparse_uncorrelated', 'make_spd_matrix', 'make_swiss_roll']
from sklearn.datasets import load_breast_cancer
dat = load_breast_cancer()
X = dat.data
rows,cols = X.shape
X.shape
(569, 30)
import math
sigma = 10
W = np.zeros((rows,rows))
for r1 in range(0,rows):
for r2 in range(0,rows):
# compute distance between row r1 and row r2
xi = X[r1]
xj = X[r2]
W[r1,r2] = math.exp(-1/2/sigma**2*np.linalg.norm(xi-xj)**2)
from matplotlib.pyplot import *
M_z = np.ones((rows,rows))-np.diag(np.ones(rows))
imshow(W*M_z);
colorbar();
from sklearn.datasets import load_iris
dat = load_iris()
X = dat.data
rows,cols = X.shape
Using Covariance matrix as a Weighted adjacency matrix¶
Consider the choice $\mathbf W = \mathbf C \propto \mathbf X \mathbf X^T$
What is $W_{ij}$ in terms of data samples?
Note relationship to distance
Do this also for the IRIS or other dataset.
II. Gaussian Graphical Models¶
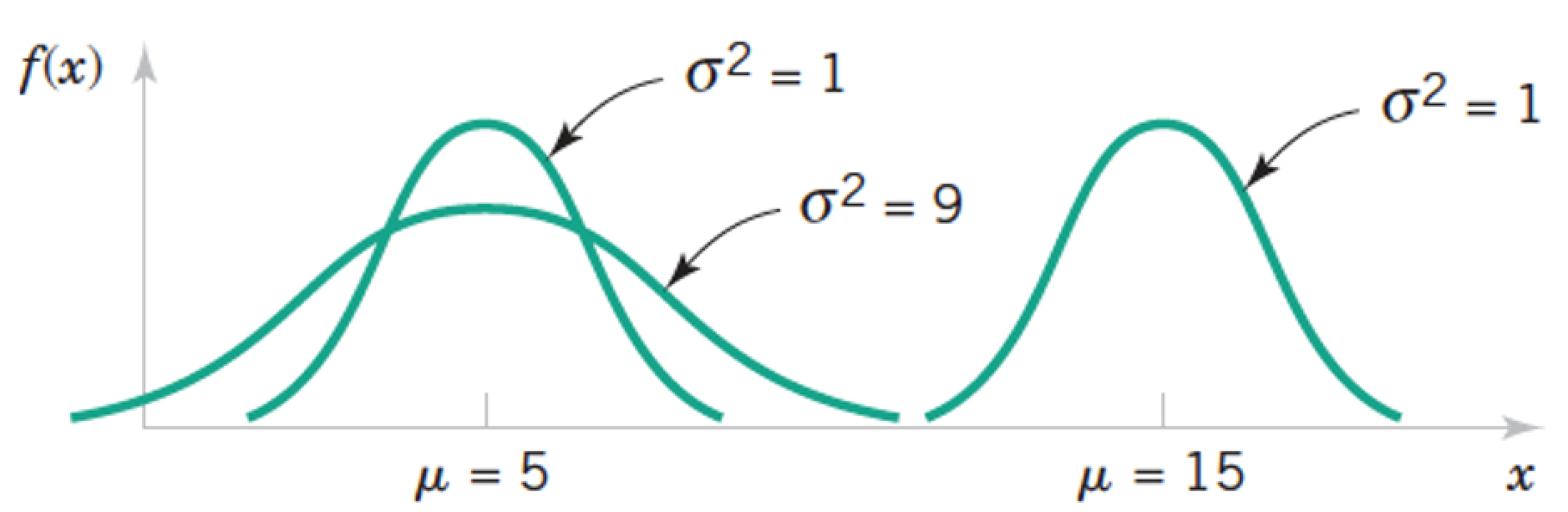
Review: Normal a.k.a. Gaussian Distribution $X \sim N(\mu, \sigma) = G(\mu, \sigma)$¶
$$ f(x) = \frac{1}{\sigma \sqrt{2 \pi}} exp \left(- \frac{(x - \mu)^2}{2 \sigma^2} \right) \text{, for } x \in R $$
import numpy as np
from matplotlib import pyplot as plt
def univariate_normal(x, mean, var):
return ((1. / np.sqrt(2 * np.pi * var)) * np.exp(-(x - mean)**2 / (2 * var)))
x = np.linspace(-5,5,1000)
plt.plot(x,univariate_normal(x,1,2));
plt.show()
Review: Joint Distributions¶
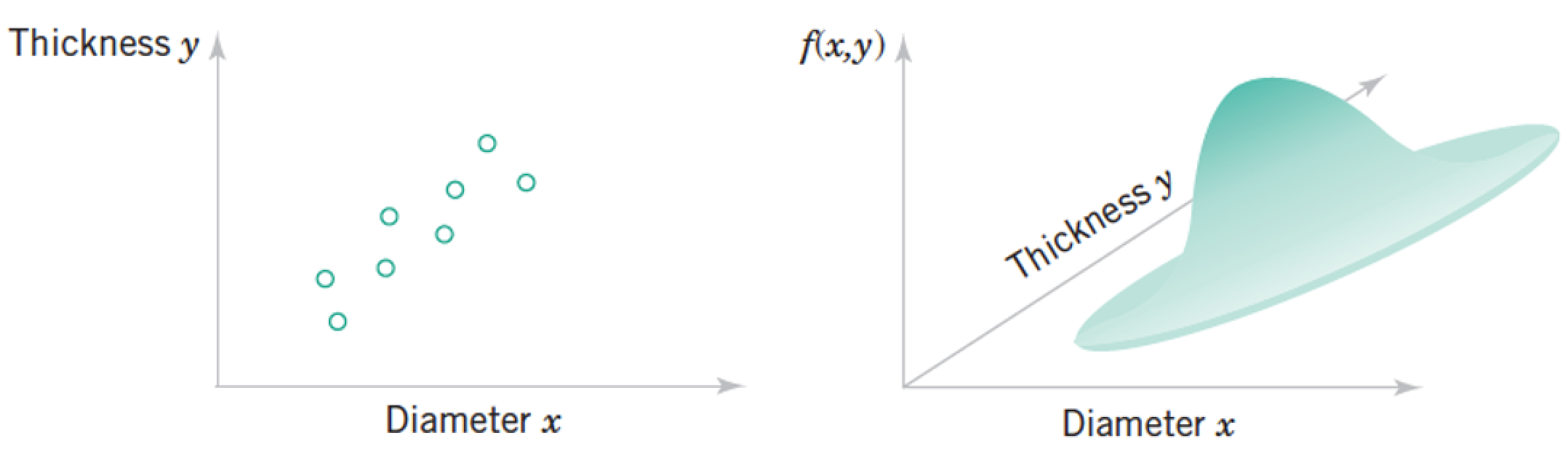
Each "sample" as a list of features, which we model as a vector of random variables, $ \mathbf x = \begin{pmatrix} Diameter \\ Thickness \end{pmatrix}¶
\begin{pmatrix} x_1 \\ \vdots \\ x_n \\ \end{pmatrix} $
Each point in the distribution is simultanous probability of all the features taking the particular vector of numbers at the point.
Multivariate Data - describing relationships¶
"Multivariate" dataset ~ a matrix with samples for rows and features for columns. Each column (a.k.a. feature) is also known as a variable.
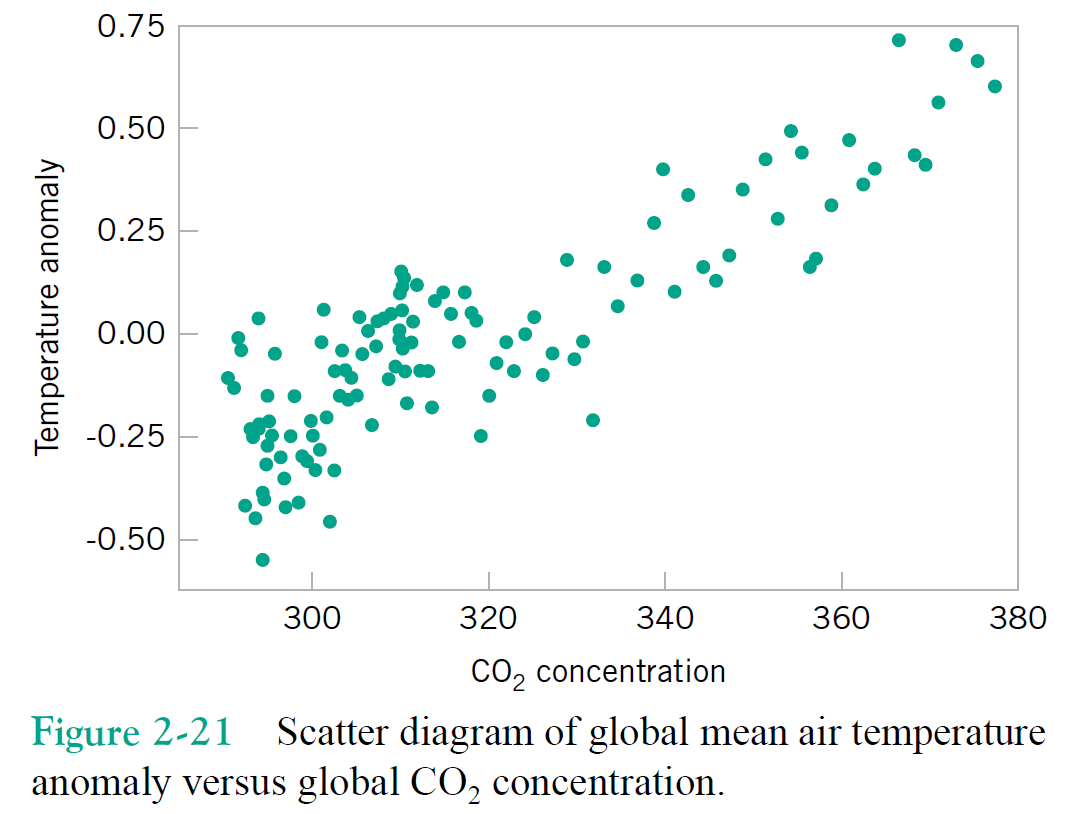
Just focusing on two variables for the moment, say column1 = $x$, and column2 = $y$.
Correlation(s)¶
\begin{align} \text{Variance} &= s^2 = \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n - 1} = \frac{\sum_{i=1}^n x_i^2 - \frac{1}{n}(\sum_{i=1}^n x_i)^2}{n - 1} \\ \text{Standard deviation} &= \sqrt{\text{Variance}} \end{align}
\begin{align} \text{Correlation Coefficient} &= r = \frac{ \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n(x_i - \bar{x})^2}\sqrt{\sum_{i=1}^n(y_i - \bar{y})^2}} = \frac{S_{xy}}{\sqrt{S_{xx} S_{yy}}} \\ %\text{''Corrected Correlation''} % &= S_{xy} = \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) % = \sum_{i=1}^n x_i y_i - \frac{1}{n}(\sum_{i=1}^n x_i)(\sum_{i=1}^n y_i) \\ \text{Covariance} &= S_{xy} = \frac{1}{n-1}\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) % = \sum_{i=1}^n x_i y_i - \frac{1}{n}(\sum_{i=1}^n x_i)(\sum_{i=1}^n y_i) \end{align}
Look kind of familiar? Relate to variance. Note $"Cov(x,x)" = S_{xx}= \sigma_x^2$.
Exercises¶
\begin{align} \text{Correlation Coefficient} &= r = \frac{ \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n(x_i - \bar{x})^2}\sqrt{\sum_{i=1}^n(x_i - \bar{x})^2}} = \frac{S_{xy}}{\sqrt{S_{xx} S_{yy}}} \end{align}
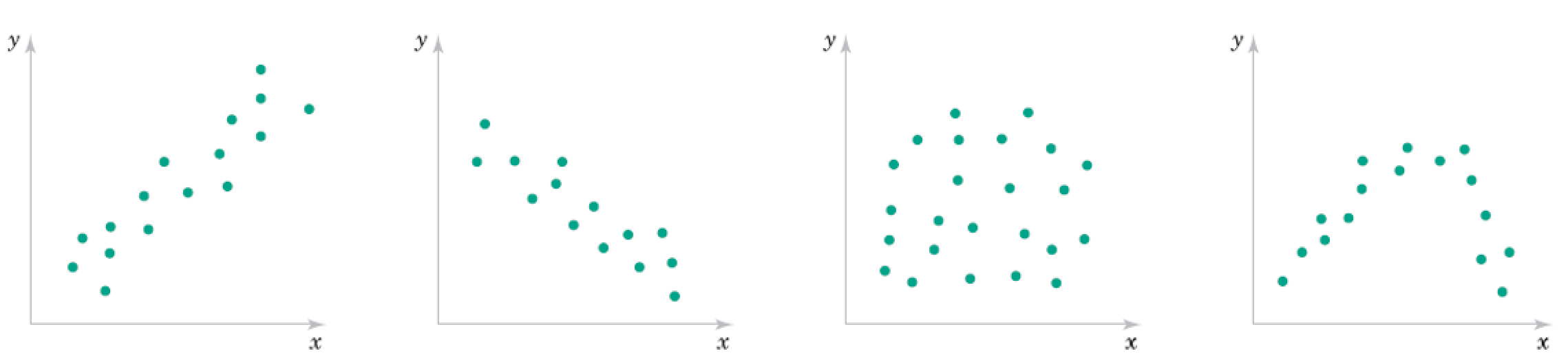
Roughly what are the correlation coefficients here?
Correlation Qualitative Behavior¶
- What does magnitude tell you about the relationship?
- What does sign tell you about the relationship?
- Would you expect the Covariance to be similar?
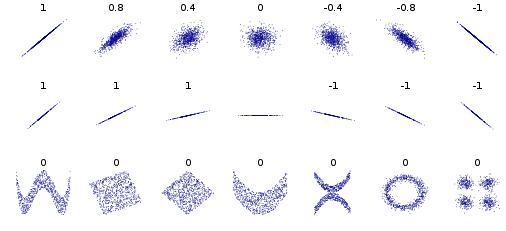
Multivariate Gaussian (for $n$ dimensions)¶
$$ f(\mathbf x) = \frac{1}{ \sqrt{2 \pi^n |\boldsymbol\Sigma|}} \exp \left(- \frac{1}{2} (\mathbf x - \boldsymbol \mu)^T \boldsymbol\Sigma^{-1} (\mathbf x - \boldsymbol \mu) \right) \text{, for } \mathbf x \in R^n $$
- Mean vector as centroid of distribution
- Covariance matrix describes spread - correlations between variables $\Sigma_{ij} = S_{\mathbf x_i \mathbf x_j}$
\begin{align} \text{Correlation Coefficient} &= r = \frac{ \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n(x_i - \bar{x})^2}\sqrt{\sum_{i=1}^n(y_i - \bar{y})^2}} = \frac{S_{xy}}{\sqrt{S_{xx} S_{yy}}} \\ %\text{''Corrected Correlation''} % &= S_{xy} = \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) % = \sum_{i=1}^n x_i y_i - \frac{1}{n}(\sum_{i=1}^n x_i)(\sum_{i=1}^n y_i) \\ \text{Covariance} &= S_{xy} = \frac{1}{n-1}\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) % = \sum_{i=1}^n x_i y_i - \frac{1}{n}(\sum_{i=1}^n x_i)(\sum_{i=1}^n y_i) \end{align}
...Terminology note...¶
In general terms, covariance is a kind of metric for correlation.
Formal definition of correlation (i.e. Pearson) differs from covariance only in scaling, so that it ranges between $\pm 1$ rather than some max and min.
I will tend to use them interchangeably, where correlation means the more intuitive concept and covariance the formal matrix we compute (or its elements).
def multivariate_normal(x, n, mean, cov):
return (1./(np.sqrt((2*np.pi)**n * np.linalg.det(cov))) * np.exp(-1/2*(x - mean).T@np.linalg.inv(cov)@(x - mean)))
mean = np.array([35,70])
cov = 100*np.array([[1,.5],[.5,1]])
pic = np.zeros((100,100))
for x1 in np.arange(0,100):
for x2 in np.arange(0,100):
x = [x1,x2]
pic[x1,x2] = multivariate_normal(x, 2, mean, cov)
plt.contour(pic);
cov
array([[100., 50.],
[ 50., 100.]])
np.linalg.inv(cov)
array([[ 0.01333333, -0.00666667],
[-0.00666667, 0.01333333]])
Exercise: independence of random variables¶
$$P(x_1,x_2) = P(x_1)P(x_2)$$
What does the mean for a multivariate Gaussian distribution?
Exercise: 2D Normal distribution¶
Can you approximate the above scatter plots with Normal distributions.
Precision and Precision Matrix¶
The Precision of a variable is commonly (though not always) defined as the inverse of the variance. $p = \sigma^{-2}$.
Higher spread means higher variance and hence lower precision.
The Precision Matrix is the inverse of the Covariance matrix. $\mathbf P = \boldsymbol\Sigma^{-1}$.
This matrix is used in the multivariate Gaussian.
Gaussian graphical models¶
Recall from Bayesian networks that correlation does not imply causation.
It is much more interesting to describe the conditional correlation (a.k.a. partial correlation) between variables, rather than simply the correlation.
If conditional correlation is zero, the variables are conditionally independent.
Amazingly, partial correlations are closely-related to the inverse of the covariance matrix, $\mathbf\Sigma^{-1}$, also called the precision matrix.
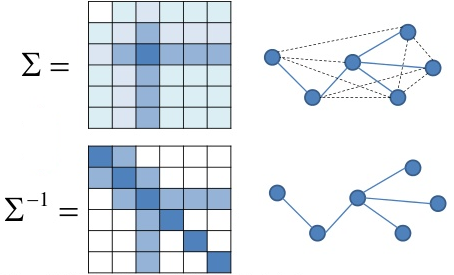
Also known as Gauss Markov Random Fields
Partial correlation and precision matrix¶
The partial correlation between a pair of variables, conditioned on all the rest, is related (within a scalar) to the $(i,j)$th element of the precision matrix.
\begin{align} \rho_{i,j} = -\frac{\sigma^{i,j}}{\sqrt{\sigma^{i,i}\sigma^{j,j}}} \end{align}
Hence a pair of variables $x_i$ and $x_j$ are conditionally independent if $\sigma^{(i,j)}=0$.
A zero implies conditional independence for a variety of non-Gaussian cases also
Recap¶
We start by considering a set of random variables $\{x_1, ..., x_m\}$
In practice we will use a vector of samples of each of the random variables $\{\mathbf x_1, ..., \mathbf x_m\}$
We like to create a matrix of data $\mathbf X$ from the vectors, where rows are samples and columns are features
If we subtract the means from each row, we can compute a sample covariance matrix $\mathbf C = \frac{1}{N-1} \mathbf X \mathbf X^T$. (often we ignore the scalar term).
If $\mathbf C$ is invertible, we can estimate the precision matrix $P = \mathbf C^{-1}$.
Nonzero elements of the precision matrix $\sigma^{i,j}$ give edges in the graphical model.
However generally hard zeros don't occur in real data calculations. Instead of thresholding the covariance matrix to make a sparse network, we can threshold the precision matrix.
Exercise: try this with your dataset. Relate to the correlation approach.¶
Graphical Lasso¶
Instead of thresholding the precision matrix values, we can seek a sparse (approximate) inverse to $\mathbf C$
\begin{align} f(\mathbf x) &= \frac{1}{ \sqrt{2 \pi^n |\boldsymbol\Sigma|}} \exp \left(- \frac{1}{2} (\mathbf x - \boldsymbol \mu)^T \boldsymbol\Sigma^{-1} (\mathbf x - \boldsymbol \mu) \right) \\ &= \frac{\sqrt{|\boldsymbol\Omega|}}{ \sqrt{2 \pi^n }} \exp \left(- \frac{1}{2} (\mathbf x - \boldsymbol \mu)^T \boldsymbol\Omega (\mathbf x - \boldsymbol \mu) \right) \\ &= \frac{\sqrt{|\boldsymbol\Omega|}}{ \sqrt{2 \pi^n }} \exp \left(- \frac{1}{2} \text{trace}(\mathbf S \boldsymbol\Omega)\right) \end{align}
Where now $\mathbf S$ is the sample covariance matrix and $\boldsymbol\Omega$ is the precision matrix (whice we view as approximations to $\boldsymbol\Sigma$ and $\boldsymbol\Sigma^{-1}$, respectively)
Graphical Lasso - continued¶
Now we view $\boldsymbol\Omega$ as the random variable and $\mathbf S$ as the data, so we have the likelihood
\begin{align} P(\mathbf S|\boldsymbol\Omega) = f(\mathbf x) = &= \frac{\sqrt{|\boldsymbol\Omega|}}{ \sqrt{2 \pi^n }} \exp \left(- \frac{1}{2} \text{trace}(\mathbf S \boldsymbol\Omega)\right) \end{align}
We wish to compute a sparse estimate for $\boldsymbol\Omega$ so use the prior $p(\lambda\boldsymbol\Omega) \propto \exp(\Vert\boldsymbol\Omega\Vert_1)$ and Bayes law to compute
\begin{align} P(\boldsymbol\Omega |\mathbf S) &= \frac{P(\mathbf S|\boldsymbol\Omega) P(\boldsymbol\Omega)}{P(\mathbf S)} \end{align}
The maximum likelihood solution, subject to a constraint that $\boldsymbol\Omega$ has non-negative eigenvalues (hence is a legitimate precision matrix):
\begin{align} \arg\max_{\boldsymbol\Omega \succeq 0} P(\boldsymbol\Omega |\mathbf S) &= \arg\max_{\boldsymbol\Omega \succeq 0} \frac{P(\mathbf S|\boldsymbol\Omega) P(\boldsymbol\Omega)}{P(\mathbf S)} \\ &= \arg\max_{\boldsymbol\Omega \succeq 0} P(\mathbf S|\boldsymbol\Omega) P(\boldsymbol\Omega) \\ &= \arg\max_{\boldsymbol\Omega \succeq 0} \log\{ P(\mathbf S|\boldsymbol\Omega) P(\boldsymbol\Omega) \} \\ &= \arg\max_{\boldsymbol\Omega \succeq 0} \{ \log|\boldsymbol\Omega| - \text{trace}(\mathbf S \boldsymbol\Omega) - \lambda\Vert\boldsymbol\Omega\Vert_1 \}\\ \end{align}
Long story short¶
compute covariance matrix of data, $\mathbf S$
Choose hyperparameter $\lambda$ to tune sparse prior (higher=sparser) and compute optimal $\arg\max_{\boldsymbol\Omega \succeq 0} \{ \log|\boldsymbol\Omega| - \text{trace}(\mathbf S \boldsymbol\Omega) - \lambda\Vert\boldsymbol\Omega\Vert_1 \}$
Form graph given that nonzero elements of $\boldsymbol\Omega$ mean conditional independence.
Example¶
Friedman and Hastie and Tibshirani "Sparse inverse covariance estimation with the graphical lasso", Biostatistics 2008
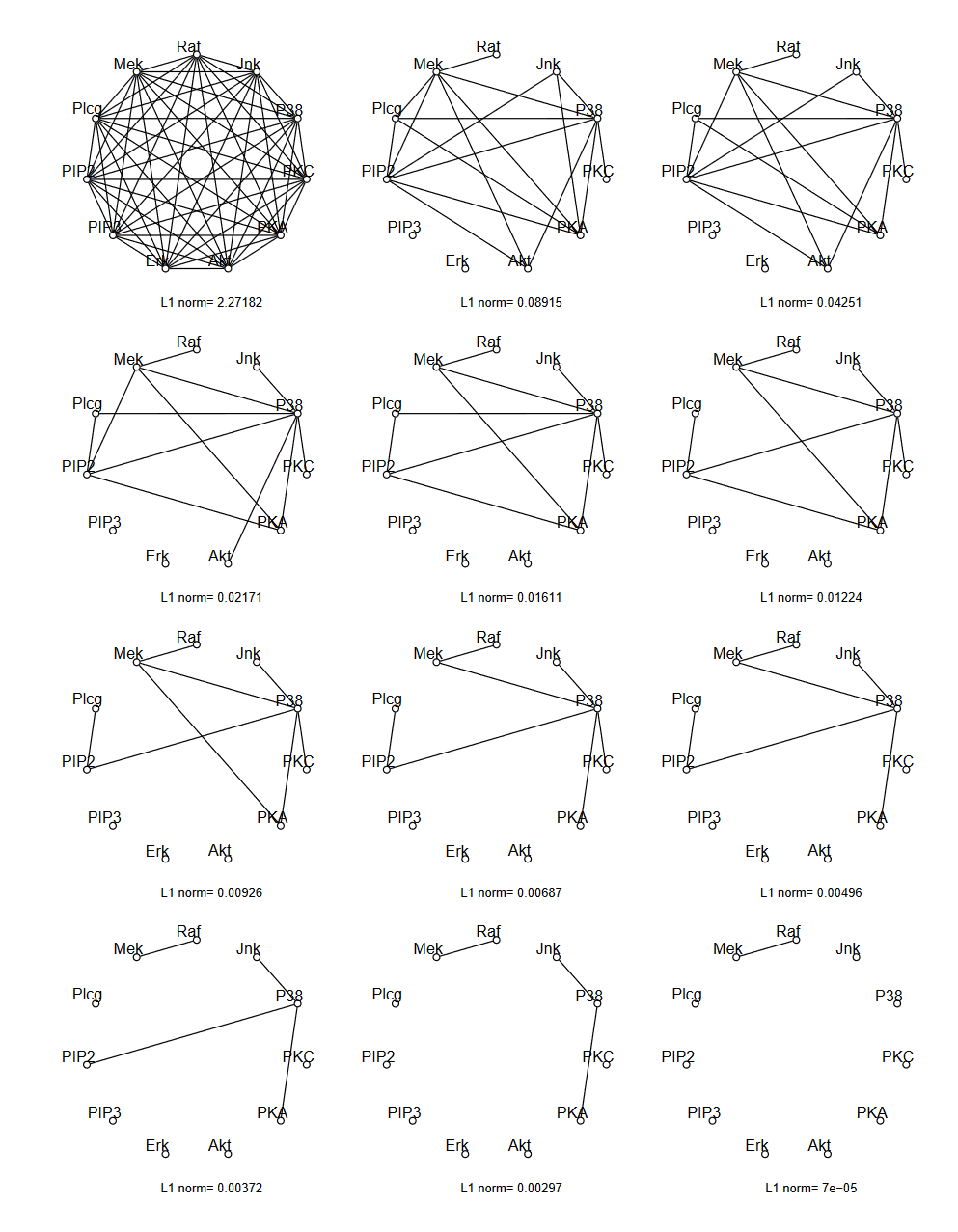
Regression approach: Neighborhood estimation problem¶
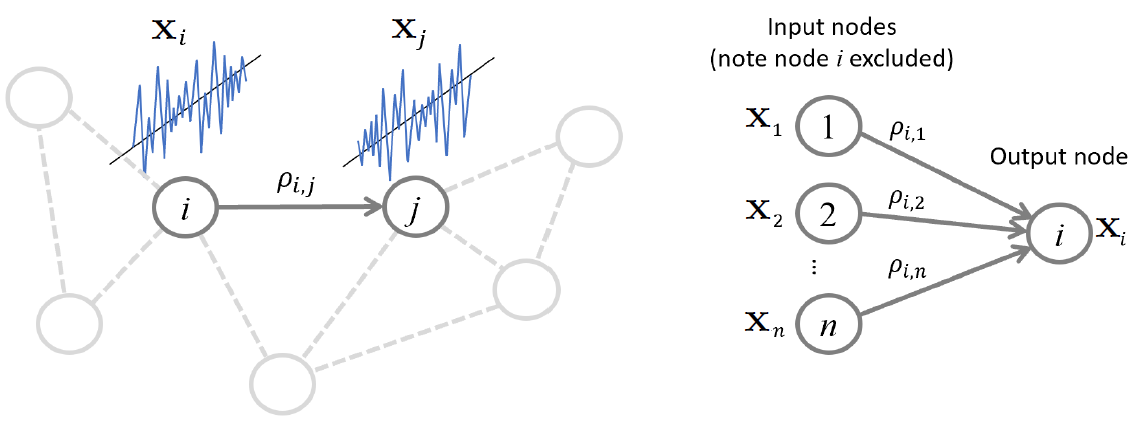
Regression problem for relating all other variables to a given variable
\begin{align} x_i = \sum_{k \neq i} \beta_{i,k} x_k + \epsilon_i, \end{align}
Partial correlation, precision matrix, and regression coefficients¶
The partial correlation between a pair of variables, conditioned on all the rest, is related by a scalar to the $(i,j)$th element of the precision matrix.
A pair of variables $x_i$ and $x_j$ are conditionally independent if the linear regression coefficient $\beta_{i,j}=0$.
\begin{align} \rho_{i,j} = -\frac{\sigma^{i,j}}{\sqrt{\sigma^{i,i}\sigma^{j,j}}} &= -\beta_{i,j} \sqrt{\frac{\sigma^{i,i}}{\sigma^{j,j}}}, \end{align}
Regression-based methods for estimating edges¶
Loop over all nodes and regress versus all others using your favorite regression method
can impose sparsity and other priors, can use efficient greedy methods
Linear Algebra view of Regression¶
The regression problem relating random variables $x_i$ is
\begin{align} x_i = \sum_{k \neq i} \beta_{i,k} x_k + \epsilon_i, \end{align}
We use a vector of samples of each of the random variables $\{\mathbf x_1, ..., \mathbf x_m\}$
Then each neighborhood regression problem is
\begin{align} \mathbf x_i = \sum_{k \neq i} \mathbf x_k \beta_{i,k} + \boldsymbol\epsilon_i, \end{align}
If we don't exclude the $i$th node from the sum (effectively allowing self-loops) we can write
\begin{align} \mathbf x_i = \mathbf X^T \boldsymbol\beta_{i} + \boldsymbol\epsilon_i, \end{align}
Using matrix of data $\mathbf X$ where rows are samples $\mathbf x_i^T$ and columns are features. And $\boldsymbol\beta_{i}$ is the vector of coefficients $\beta_{i,k}$ relating the other nodes to the $i$th node.
Exercises¶
Draw a little network and relate it to $\mathbf X$ and $\boldsymbol\beta_{i}$
Combine all the regression problems for all nodes into a single equation
Least squares solution¶
Suppose our dataset matrix $\mathbf X$ is not invertible.
The least squares solution to $\mathbf X^T \mathbf B = \mathbf X^T$ is $\mathbf B = (\mathbf X^T)^\dagger \mathbf X^T$ using the pseudoinverse
If the SVD of $\mathbf X^T$ is $\mathbf U \mathbf S \mathbf V^T$ then we can write the SVD of $(\mathbf X^T)^\dagger$ as $\mathbf V \mathbf S\dagger \mathbf U^T$, where $S\dagger$ is a rectangular diagonal matrix with the inverses of the nonzero singular values of $\mathbf X^T$ on the diagonal (and zero otherwise).
Multiplying this out we get
\begin{align} \mathbf B &= (\mathbf X^T)^\dagger \mathbf X^T \\ &= (\mathbf V \mathbf S^\dagger \mathbf U^T)(\mathbf U \mathbf S \mathbf V^T) \\ &= \mathbf U_r \mathbf U_r^T \end{align}
where $\mathbf U_r$ is the matrix of singular vectors for the $r$ nonzero singular values of $\mathbf X^T$.
Regression as Embedding¶
Consider the distances between rows of the matrix of regression coefficients $\mathbf B = \mathbf U_r \mathbf U_r^T $
\begin{align} d(i,j) &= \Vert \mathbf b^{(i)} - \mathbf b^{(j)} \Vert \\ &= \Vert \mathbf u_r^{(i)} \mathbf U_r^T - \mathbf u_r^{(j)} \mathbf U_r^T \Vert \\ &= \Vert (\mathbf u_r^{(i)} - \mathbf u_r^{(j)}) \mathbf U_r^T \Vert \\ &= \Vert \mathbf u_r^{(i)} - \mathbf u_r^{(j)} \Vert \\ \end{align} Where we use the fact that an orthogonal transformation does not change the distance (with a $\ell_2$-norm)
So the regression coefficient matrix is equivalent to a particular case of spectral embedding of the data
Breast Cancer Data exercise¶
Visualize the network using thresholded covariance
Visualize using precision matrix bia GraphicalLasso
from sklearn import datasets
dat = datasets.load_breast_cancer()
Network based on Covariance of features¶
plt.imshow(C)
plt.colorbar();
Now visualize network¶
Covariance of Features for Malignant tumors¶
network0()
Covariance of Features for Benign tumors¶
network0()
Scikit-Learn GraphicalLasso()¶
import numpy as np
from sklearn.covariance import GraphicalLasso
Precision matrix of Features for Malignant tumors¶
network0()
Precision matrix of Features for Benign tumors¶
network0()
# author: Gael Varoquaux <gael.varoquaux@inria.fr>
# License: BSD 3 clause
# Copyright: INRIA
import numpy as np
from scipy import linalg
from sklearn.datasets import make_sparse_spd_matrix
from sklearn.covariance import GraphicalLassoCV, ledoit_wolf
import matplotlib.pyplot as plt
def rundemo():
# #############################################################################
# Generate the data
n_samples = 60
n_features = 20
prng = np.random.RandomState(1)
prec = make_sparse_spd_matrix(n_features, alpha=.98,
smallest_coef=.4,
largest_coef=.7,
random_state=prng)
cov = linalg.inv(prec)
d = np.sqrt(np.diag(cov))
cov /= d
cov /= d[:, np.newaxis]
prec *= d
prec *= d[:, np.newaxis]
X = prng.multivariate_normal(np.zeros(n_features), cov, size=n_samples)
X -= X.mean(axis=0)
X /= X.std(axis=0)
# #############################################################################
# Estimate the covariance
emp_cov = np.dot(X.T, X) / n_samples
model = GraphicalLassoCV(cv=5)
model.fit(X)
cov_ = model.covariance_
prec_ = model.precision_
lw_cov_, _ = ledoit_wolf(X)
lw_prec_ = linalg.inv(lw_cov_)
# #############################################################################
# Plot the results
plt.figure(figsize=(10, 6))
plt.subplots_adjust(left=0.02, right=0.98)
# plot the covariances
covs = [('Empirical', emp_cov), ('Ledoit-Wolf', lw_cov_),
('GraphicalLassoCV', cov_), ('True', cov)]
vmax = cov_.max()
for i, (name, this_cov) in enumerate(covs):
plt.subplot(2, 4, i + 1)
plt.imshow(this_cov, interpolation='nearest', vmin=-vmax, vmax=vmax,
cmap=plt.cm.RdBu_r)
plt.xticks(())
plt.yticks(())
plt.title('%s covariance' % name)
# plot the precisions
precs = [('Empirical', linalg.inv(emp_cov)), ('Ledoit-Wolf', lw_prec_),
('GraphicalLasso', prec_), ('True', prec)]
vmax = .9 * prec_.max()
for i, (name, this_prec) in enumerate(precs):
ax = plt.subplot(2, 4, i + 5)
plt.imshow(np.ma.masked_equal(this_prec, 0),
interpolation='nearest', vmin=-vmax, vmax=vmax,
cmap=plt.cm.RdBu_r)
plt.xticks(())
plt.yticks(())
plt.title('%s precision' % name)
if hasattr(ax, 'set_facecolor'):
ax.set_facecolor('.7')
else:
ax.set_axis_bgcolor('.7')
# plot the model selection metric
plt.figure(figsize=(4, 3))
plt.axes([.2, .15, .75, .7])
plt.plot(model.cv_alphas_, np.mean(model.grid_scores_, axis=1), 'o-')
plt.axvline(model.alpha_, color='.5')
plt.title('Model selection')
plt.ylabel('Cross-validation score')
plt.xlabel('alpha')
plt.show()
rundemo()
Sklearn Demo: Visualizing the stock market structure¶
Use is the daily variation in quote price to relate stocks: quotes that are linked tend to cofluctuate during a day.
Use sparse inverse covariance estimation to find which quotes are correlated conditionally on the others. Specifically, sparse inverse covariance gives us a graph, that is a list of connection. For each symbol, the symbols that it is connected too are those useful to explain its fluctuations.
# Author: Gael Varoquaux gael.varoquaux@normalesup.org
# License: BSD 3 clause
import sys
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection
import pandas as pd
from sklearn import cluster, covariance, manifold
print(__doc__)
# #############################################################################
# Retrieve the data from Internet
# The data is from 2003 - 2008. This is reasonably calm: (not too long ago so
# that we get high-tech firms, and before the 2008 crash). This kind of
# historical data can be obtained for from APIs like the quandl.com and
# alphavantage.co ones.
symbol_dict = {
'TOT': 'Total',
'XOM': 'Exxon',
'CVX': 'Chevron',
'COP': 'ConocoPhillips',
'VLO': 'Valero Energy',
'MSFT': 'Microsoft',
'IBM': 'IBM',
'TWX': 'Time Warner',
'CMCSA': 'Comcast',
'CVC': 'Cablevision',
'YHOO': 'Yahoo',
'DELL': 'Dell',
'HPQ': 'HP',
'AMZN': 'Amazon',
'TM': 'Toyota',
'CAJ': 'Canon',
'SNE': 'Sony',
'F': 'Ford',
'HMC': 'Honda',
'NAV': 'Navistar',
'NOC': 'Northrop Grumman',
'BA': 'Boeing',
'KO': 'Coca Cola',
'MMM': '3M',
'MCD': 'McDonald\'s',
'PEP': 'Pepsi',
'K': 'Kellogg',
'UN': 'Unilever',
'MAR': 'Marriott',
'PG': 'Procter Gamble',
'CL': 'Colgate-Palmolive',
'GE': 'General Electrics',
'WFC': 'Wells Fargo',
'JPM': 'JPMorgan Chase',
'AIG': 'AIG',
'AXP': 'American express',
'BAC': 'Bank of America',
'GS': 'Goldman Sachs',
'AAPL': 'Apple',
'SAP': 'SAP',
'CSCO': 'Cisco',
'TXN': 'Texas Instruments',
'XRX': 'Xerox',
'WMT': 'Wal-Mart',
'HD': 'Home Depot',
'GSK': 'GlaxoSmithKline',
'PFE': 'Pfizer',
'SNY': 'Sanofi-Aventis',
'NVS': 'Novartis',
'KMB': 'Kimberly-Clark',
'R': 'Ryder',
'GD': 'General Dynamics',
'RTN': 'Raytheon',
'CVS': 'CVS',
'CAT': 'Caterpillar',
'DD': 'DuPont de Nemours'}
symbols, names = np.array(sorted(symbol_dict.items())).T
quotes = []
for symbol in symbols:
print('Fetching quote history for %r' % symbol, file=sys.stderr)
url = ('https://raw.githubusercontent.com/scikit-learn/examples-data/'
'master/financial-data/{}.csv')
quotes.append(pd.read_csv(url.format(symbol)))
close_prices = np.vstack([q['close'] for q in quotes])
open_prices = np.vstack([q['open'] for q in quotes])
# The daily variations of the quotes are what carry most information
variation = close_prices - open_prices
# #############################################################################
# Learn a graphical structure from the correlations
edge_model = covariance.GraphicalLassoCV(cv=5)
# standardize the time series: using correlations rather than covariance
# is more efficient for structure recovery
X = variation.copy().T
X /= X.std(axis=0)
edge_model.fit(X)
# #############################################################################
# Cluster using affinity propagation
_, labels = cluster.affinity_propagation(edge_model.covariance_)
n_labels = labels.max()
for i in range(n_labels + 1):
print('Cluster %i: %s' % ((i + 1), ', '.join(names[labels == i])))
# #############################################################################
# Find a low-dimension embedding for visualization: find the best position of
# the nodes (the stocks) on a 2D plane
# We use a dense eigen_solver to achieve reproducibility (arpack is
# initiated with random vectors that we don't control). In addition, we
# use a large number of neighbors to capture the large-scale structure.
node_position_model = manifold.LocallyLinearEmbedding(
n_components=2, eigen_solver='dense', n_neighbors=6)
embedding = node_position_model.fit_transform(X.T).T
# #############################################################################
# Visualization
plt.figure(1, facecolor='w', figsize=(10, 8))
plt.clf()
ax = plt.axes([0., 0., 1., 1.])
plt.axis('off')
# Display a graph of the partial correlations
partial_correlations = edge_model.precision_.copy()
d = 1 / np.sqrt(np.diag(partial_correlations))
partial_correlations *= d
partial_correlations *= d[:, np.newaxis]
non_zero = (np.abs(np.triu(partial_correlations, k=1)) > 0.02)
# Plot the nodes using the coordinates of our embedding
plt.scatter(embedding[0], embedding[1], s=100 * d ** 2, c=labels,
cmap=plt.cm.nipy_spectral)
# Plot the edges
start_idx, end_idx = np.where(non_zero)
# a sequence of (*line0*, *line1*, *line2*), where::
# linen = (x0, y0), (x1, y1), ... (xm, ym)
segments = [[embedding[:, start], embedding[:, stop]]
for start, stop in zip(start_idx, end_idx)]
values = np.abs(partial_correlations[non_zero])
lc = LineCollection(segments,
zorder=0, cmap=plt.cm.hot_r,
norm=plt.Normalize(0, .7 * values.max()))
lc.set_array(values)
lc.set_linewidths(15 * values)
ax.add_collection(lc)
# Add a label to each node. The challenge here is that we want to
# position the labels to avoid overlap with other labels
for index, (name, label, (x, y)) in enumerate(
zip(names, labels, embedding.T)):
dx = x - embedding[0]
dx[index] = 1
dy = y - embedding[1]
dy[index] = 1
this_dx = dx[np.argmin(np.abs(dy))]
this_dy = dy[np.argmin(np.abs(dx))]
if this_dx > 0:
horizontalalignment = 'left'
x = x + .002
else:
horizontalalignment = 'right'
x = x - .002
if this_dy > 0:
verticalalignment = 'bottom'
y = y + .002
else:
verticalalignment = 'top'
y = y - .002
plt.text(x, y, name, size=10,
horizontalalignment=horizontalalignment,
verticalalignment=verticalalignment,
bbox=dict(facecolor='w',
edgecolor=plt.cm.nipy_spectral(label / float(n_labels)),
alpha=.6))
plt.xlim(embedding[0].min() - .15 * embedding[0].ptp(),
embedding[0].max() + .10 * embedding[0].ptp(),)
plt.ylim(embedding[1].min() - .03 * embedding[1].ptp(),
embedding[1].max() + .03 * embedding[1].ptp())
plt.show()
Automatically created module for IPython interactive environment
Fetching quote history for 'AAPL' Fetching quote history for 'AIG' Fetching quote history for 'AMZN' Fetching quote history for 'AXP' Fetching quote history for 'BA' Fetching quote history for 'BAC' Fetching quote history for 'CAJ' Fetching quote history for 'CAT' Fetching quote history for 'CL' Fetching quote history for 'CMCSA' Fetching quote history for 'COP' Fetching quote history for 'CSCO' Fetching quote history for 'CVC' Fetching quote history for 'CVS' Fetching quote history for 'CVX' Fetching quote history for 'DD' Fetching quote history for 'DELL' Fetching quote history for 'F' Fetching quote history for 'GD' Fetching quote history for 'GE' Fetching quote history for 'GS' Fetching quote history for 'GSK' Fetching quote history for 'HD' Fetching quote history for 'HMC' Fetching quote history for 'HPQ' Fetching quote history for 'IBM' Fetching quote history for 'JPM' Fetching quote history for 'K' Fetching quote history for 'KMB' Fetching quote history for 'KO' Fetching quote history for 'MAR' Fetching quote history for 'MCD' Fetching quote history for 'MMM' Fetching quote history for 'MSFT' Fetching quote history for 'NAV' Fetching quote history for 'NOC' Fetching quote history for 'NVS' Fetching quote history for 'PEP' Fetching quote history for 'PFE' Fetching quote history for 'PG' Fetching quote history for 'R' Fetching quote history for 'RTN' Fetching quote history for 'SAP' Fetching quote history for 'SNE' Fetching quote history for 'SNY' Fetching quote history for 'TM' Fetching quote history for 'TOT' Fetching quote history for 'TWX' Fetching quote history for 'TXN' Fetching quote history for 'UN' Fetching quote history for 'VLO' Fetching quote history for 'WFC' Fetching quote history for 'WMT' Fetching quote history for 'XOM' Fetching quote history for 'XRX' Fetching quote history for 'YHOO'
Cluster 1: Apple, Amazon, Yahoo Cluster 2: Comcast, Cablevision, Time Warner Cluster 3: ConocoPhillips, Chevron, Total, Valero Energy, Exxon Cluster 4: Cisco, Dell, HP, IBM, Microsoft, SAP, Texas Instruments Cluster 5: Boeing, General Dynamics, Northrop Grumman, Raytheon Cluster 6: AIG, American express, Bank of America, Caterpillar, CVS, DuPont de Nemours, Ford, General Electrics, Goldman Sachs, Home Depot, JPMorgan Chase, Marriott, 3M, Ryder, Wells Fargo, Wal-Mart Cluster 7: McDonald's Cluster 8: GlaxoSmithKline, Novartis, Pfizer, Sanofi-Aventis, Unilever Cluster 9: Kellogg, Coca Cola, Pepsi Cluster 10: Colgate-Palmolive, Kimberly-Clark, Procter Gamble Cluster 11: Canon, Honda, Navistar, Sony, Toyota, Xerox

