Mathematical Methods for Data Science

Keith Dillon
Spring 2020

Topic 1: Introduction

also known as...

Hacking Math II

This topic:

1. Syllabus discussion
2. Basic math in python

Reading: Readings:

• "Coding the Matrix" Chapters 0 and 1.
• Tons of Jupyter and Python resources on internet.

Prerequisites

• Programming skills necessary. We will be using Python.

• Vector geometry & calculus

• Some exposure to Prob & Stat

• Undergraduate Linear Algebra

Prerequisites exist for a reason. Most people fail if they don't actually know the contents of them. If you are weak in an area you will need to devote extra time to keeping up. The university has plenty of resources for tutoring in the undergraduate subjects listed above.

You cannot cram and memorize your way through mathematics.

What is Linear Algebra ? Math 3311

Student Learning Outcomes: "After successfully completing this course the student is able to...

1. Utilize row operations and recognize row equivalence for linear systems;
2. Recognize linear dependence and independence of vectors;
3. Work with fundamental properties of matrix algebra, including matrix multiplication, matrix inverses, and transposes;
4. Compute the LU factorization of a matrix;
5. Compute the determinant of a matrix using a cofactor expansion, and recognize fundamental properties of determinants.
6. Identify algebraic invariants of matrices such as rank, nullity and the classification of subspaces associated with linear transformations;
7. Change bases and coordinates with respect to a basis; and,
8. Utilize eigenvalues and eigenvectors to diagonalize a matrix"

Math 3311 (continued)

Key topics covered include:

1. Solutions of linear systems: Systems of equations and matrix operations, row operations, row reduction and row equivalence. Solvability of systems and uniqueness of solutions. Fundamentals of matrix algebra and linear independence.
2. Determinants: Alternating multi-linear maps, permutations and cofactor expansion.
3. Vector Spaces: Vector geometry and fundamentals of vector spaces, including linear independence,bases and dimension and coordinates with respect to a basis. Row spaces, column space, and null space. Rank and nullity. Subspaces.
4. Orthogonality: Inner product spaces, orthonormal bases, Gram-Schmidt orthogonalization, least squares approximation, and orthogonal matrices. Norms and inner products; least squares and orthogonal projection.
5. Abstractions: Relating matrices to linear transformations and developing the properties of linear operators, coordinate systems and transformations, the characteristic equation, and diagonalizability.
6. Algebraic aspects: Eigenvalues and eigenvectors.

Grading

• Quizzes/Homework/Labs/Participation - 10%
• Midterm I - 25%
• Midterm II - 30%
• Final Exam - 35%

Text

• “Linear Algebra and Learning from Data”, Gilbert Strang, Wellesley-Cambridge Press 2019
• "Coding the Matrix", Philim Klein, Newtonian Press 2013 (optional)
• other sources will be cited as used

Notes vs. Slides

Slides are a prop to help discussions and lectures, not a replacement for notes.

Math does not work well via slides. Derivations and problems will be often be given only on the board, requiring note-taking.

If you have a computer science background this is a skill you may need to re-learn.

When you ask "what will be on the exam", I will say "the topics I emphasized in class".

Attendance

"The instructor has the right to dismiss from class any student who has been absent more than two weeks (pro-rated for terms different from that of the semester). A dismissed student will receive a withdrawal (W) from the course if they are still eligible for a withdrawal per the University “Withdrawal from a Course” policy, or a failure (F) if not." - Student Handbook

If you don't attend class you are responsible for learning the material on your own.

If you are becoming a burden on the class due to absences I will have you removed.

Participation

Active-learning techniques will be used regularly in class, requiring students to work individually and/or with other students.

Refusal to participate (or consistent failure to pay attention) will be treated as absence from class and ultimately lead to dismissal from the class.

Topics

1. Linear Algebra with Python
2. Dimensionality Reduction and applications of the SVD
3. Numerical Mathematics
4. Calculus for Machine Learning
5. Optimization for Machine Learning

II. Basic Math in Python

Jupyter - "notebooks" for inline code + LaTex math + markup, etc.

A single document containing a series of "cells". Each containing code which can be run, or images and other documentation.

• Run a cell via [shift] + [Enter] or "play" button in the menu.

Will execute code and display result below, or render markup etc.

Can also use R or Julia (easily), Matlab, SQL, etc. (with icreasing difficulty).

import datetime

print("This code is run right now (" + str(datetime.datetime.now()) + ")")

'hi'

This code is run right now (2019-01-29 18:53:42.540410)

'hi'

x=1+2+2

print(x)

5

Installation

First project: get Jupyter running and be able to import listed tools

Easiest to install via Anaconda. Preferrably Python 3.

https://www.anaconda.com/download/

Highly recomended to make a separate environment for class - hot open source tools change fast and deprecate (i.e. break) old features constantly

conda install jupyter matplotlib numpy scipy scikit-learn pandas ...

Many other packages...

Python Help Tips

• Get help on a function or object via [shift] + [tab] after the opening parenthesis function(

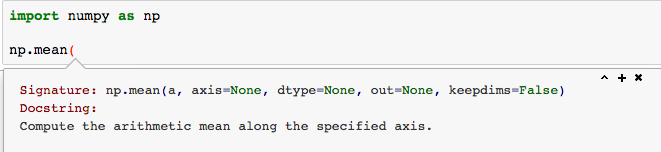
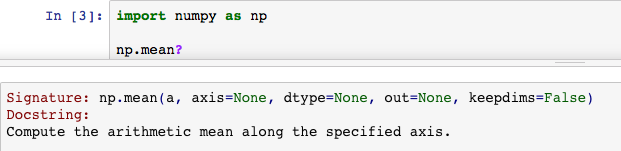
• Can also get help by executing function?

Basic Python

Reading: Chapter zero of "Coding the Matrix" (Lab at end)

• Data structures
• Programming

Basic Python Data Structures ("collections")

• Sets
• Lists
• Tuples
• Dictionaries

Sets {item1, item2, item3}

• Order is not necessarily maintained
• Each item occurs at most once
• Mutable

Create a set with a repeated value in and print it

S={1,2,2,3}
print(S)

{1, 2, 3}

Compute the cardinality of your set

print(len(S))

3

Sets ...continued

Other handy functions

• sum()
• logical test for membership
• add(), remove(), update()
• copy() -- NOTE: Python "=" binds LHS to RHS by reference, it is not a copy.

Q: Is a set a good data structure to make vectors and do linear algebra?

Lists [item1, item2, item3]

• Sequence of values - order & repeats ok
• Mutable
• Concatenate lists with "+"
• Index with mylist[index] - note zero based

Convert your set to a list, print list, its length, it's first and last elements

L = list(S)
print(L)
print("length =",len(L))
print(L[0],L[2])

[1, 2, 3]
length = 3
1 3

Slices - mylist[start:end:step]

Matlabesque way to select sub-sequences from list

• If first index is zero, can omit - mylist[:end:step]
• If last index is length-1, can omit - mylist[::step]
• If step is 1, can omit mylist[start:end]

Make slices for even and odd indexed members of your list.

Q: Is this a good data structure to make vectors and do linear algebra?

Tuples (1,2,3)

• Immutable version of list basically

(1,2,3)[1] # note can access directly

• Handy for packing info
• sometimes omit the parenthesis

1,2

(1, 2)

The constructors

• convert other collections (and iterators) into collections

L = list(S)
S = set(L)
T = tuple(S)

Dictionaries {key1:value1,key2:value2}

• key:value ~ word:definition
• access like a generalized list

mydict = {0:100,1:200,3:300}
mydict[0]

100

mydict = {'X':'hello','Y':'goodbye'}
mydict['X']

'hello'

Dictionaries ...continued

• keys()
• values()
• items()

How would you use a dictionary to make a vector?

Basic Python Programming

• Comprehensions
• Loops
• Whitespace
• Conditional statements
• Functions

Comprehensions

• Use iterators for generating sets/lists/tuples
• Similar to mathematical set notation
• popular in "Coding the Matrix"

L=list(i for i in {1,2,3})
print(L)

[1, 2, 3]

dict((mydict[key],key) for key in mydict)

{'hello': 'X', 'goodbye': 'Y'}

Iterate over list and produce list squared

L=[1,1,2,3,4,4,5]

LL = list([x,y] for x in [1,2,3] for y in [1,2,3])
LL

[[1, 1], [1, 2], [1, 3], [2, 1], [2, 2], [2, 3], [3, 1], [3, 2], [3, 3]]

Loops

for x in {1,2,3}:     
    print(x)
    print(x*x)

1
1
2
4
3
9

Whitespace

• used for grouping code
• same indent = same group
• nested code = increased indent
• must be used properly

for x in {1,2,3}: 
    print(x)
    for y in {1,2,3}: 
        print('...',x,y)

1
... 1 1
... 1 2
... 1 3
2
... 2 1
... 2 2
... 2 3
3
... 3 1
... 3 2
... 3 3

x=0
while x<5:
    print(x)
    x=x+1

0
1
2
3
4

Range Function

list(range(10,0,-1))

[10, 9, 8, 7, 6, 5, 4, 3, 2, 1]

for x in range(0,10):
    print(x)

0
1
2
3
4
5
6
7
8
9

Conditional Statements

if 2+2 == 4:     
    print('tree')

tree

Defining functions

def myfunc(x):
    print(x)
    return x**2
    
myfunc(4)

4

16

Basic Abstract Mathematics

Reading: Chapter zero of "Coding the Matrix"

• Sets
• Functions
• Procedure
• Inverse function

Sets

• Elements
• Subsets
• Cardinality
• Reals
• Cartesian products of sets

Function

• Rule that assigns input to output
• Mapping between sets
• Image
• Pre-image
• Domain
• Co-domain
• Composition
• Probablity as a function

Procedure

• Description of a computation
• Also called "function" (but not by our book)
• Versus "computational problem"

Inverse function

• Forward versus Backward Problem
• One-to-one
• Onto
• Of composition

Fields

A set with "+" and "x" operations (that work properly).

• Reals $\bf R$
• Complex numbers $\bf C$
• GF(2)

Numerical precision

• Bytes/words, ints, floats, doubles... how big are they?

• IEEE 745 standard numerical arithmetic

• nan, inf, eps

• "Hard zeros"

Vector - Multiple numbers "drawn from a field"

A $k$-dimensional vector $y$ is an ordered collection of $k$ numbers $y_1 , y_2 , . . . , y_k$ written as $\textbf{y} = (y_1,y_2,...,y_k)$.

The numbers $y_j$, for $j = 1,2,...,k$, are called the $\textbf{components}$ of the vector $y$.

Note boldface for vectors and italic for scalars.

It can be written either as rows or columns, and we won't worry about this.

$$\textbf{y} = \begin{bmatrix} y_1 \\y_2 \\ \vdots \\ y_k \end{bmatrix} = [y_1,y_2,...,y_k]^{T} $$

(Swapping rows and columns = transposing. 1st column = top. 1st row = left.)

Vector Examples

1. Coordinates

2. Direction

3. GPS entry

4. Collection of clinical study data for single individual ("sample" in machine learning).

5. An image

6. A music or voice signal

7. A block of binary data

Consider the numbers we want to use for each.

Data Science Examples of vectors

A list of data for different "dimensions", for one person, product, etc.

-Yaser Abu-Mostafa, Learning From Data

KEY FACT: The position in the vector is special, e.g. $x$ versus $y$, age versus gender.

Drawn from a Field?

Recall a field is a set. So a vector has each member from the set.

• Vector of real numbers $\mathbf v \in \mathbf R^n$

• Vector of binary numbers $\mathbf b \in GF(2)^n$

What is the notation for our previous examples?

Data Structure Options

• Python Sets
• Python Lists
• Python Tuples
• Python Dictionaries

Consider how you would use each of these to make a vector of coordinates.

Recall the other kinds of info we make into vectors. Does the data structure work for all of them?

Vector Addition $\mathbf a + \mathbf b$

Addition of two k-dimensional vectors $\textbf{x} = (x_1, x_2, ... , x_k)$ and $\textbf{y} = (y_1,y_2,...,y_k)$ is defined as a new vector $\textbf{z} = (z_1,z_2,...,z_k)$, denoted $\textbf{z} = \textbf{x}+\textbf{y}$,with components given by $z_j = x_j+y_j$.

Vector Addition $\mathbf a + \mathbf b$

Addition of corresponding entries.

Geometrical perspective.

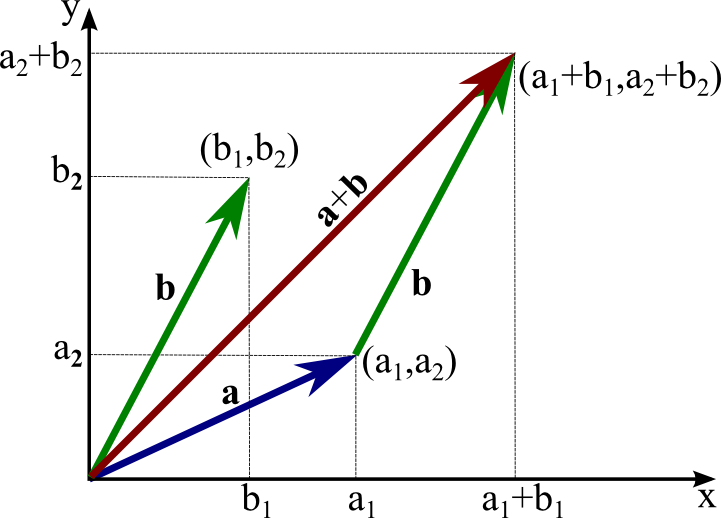
Consider in terms of applications.

Scalar-Vector multiplication $\alpha \mathbf y$

Scalar multiplication of a vector $\textbf{y} = (y_1, y_2, . . . , y_k)$ and a scalar α is defined to be a new vector $\textbf{z} = (z_1,z_2,...,z_k)$, written $\textbf{z} = \alpha\ \textbf{y}$ or $\textbf{z} = \textbf{y} \alpha$, whose components are given by $z_j = \alpha y_j$.

Code these operations in Python

Consider vectors describing distance travelled in 2D.

Make two functions:

• multiply a vector of data by a scalar (i.e. "scale it")

• add two vectors.

• Make it work for any number of dimensions

The Dot Product $\mathbf x \cdot \mathbf y$

If we have two vectors: ${\bf{x}} = (x_1, x_2, ... , x_k)$ and ${\bf{y}} = (y_1,y_2,...,y_k)$

The dot product is written: ${\bf{x}} \cdot {\bf{y}} = x_{1}y_{1}+x_{2}y_{2}+\cdots+x_{k}y_{k}$

If $\mathbf{x} \cdot \mathbf{y} = 0$ then $x$ and $y$ are orthogonal

What is $\mathbf{x} \cdot \mathbf{x}$?

Applications

• Measuring similarity

• Customer profile comparison

Applications

You may have heard of this little guy:

Code the dot product in Python

• Choose appropriate data structures for your vectors

• Make it work for any number of dimensions

Properties of Dot Product

• Commutative
• Homogeneous
• Distributes over vector addition

Test them with your code and example vectors

Homogeneity: $(\alpha \mathbf x) \cdot \mathbf y = \alpha (\mathbf x \cdot \mathbf y)$

Consider what this means for using the dot product to measure similarity.

Use your functions to implement this both ways.

Time to get serious...

Suppose your vector was extremely long but very sparse.

How would you make a "compressed" vector representation?

Make functions to scale and add such vectors

Sparse Vectors

Dense vectors are stored in a list or array where position gives index

$$[v_1,v_2,v_3] \text{ stored as } [v_1, v_2, v_3] \text{ in ordered data structure }$$

Easy to access $k$the element via startingaddress + k $\rightarrow v{k+1}$ (note zero-based indexing in computers)

Sparse vectors are stored in a compact form to save memory space, only maintain nonzero values This requires we also store the indices of these nonzero values

$$ [0,0,0,0.1,0,0,0,0.5,0,0] \text{ stored as } [(4,0.1),(8,0.5)] $$

Additional overhead required for accessing and performing operations.

Classes in Python

Clunky but handy to encapsulate related code

Note odd way that constructor is defined

Also need to pass "self" argument to every function

class Complex:
    def __init__(self, realpart, imagpart):
        self.r = realpart
        self.i = imagpart
x = Complex(3.0, -4.5)
x.r, x.i

(3.0, -4.5)

Python Lab

Make a class for "dense" vectors that contains all your functions thus far.

Add methods for handling sparse vectors:

1. Vector addition
2. Scalar-vector multiplication
3. Dot product

Compare speed to large dense vectors for different levels of density.

Advanced: compare to sparse vectors in numpy.

Matrices

A matrix $\mathbf A$ is a rectangular array of numbers, of size $m \times n$ as follows:

$\mathbf A = \begin{bmatrix} A_{1,1} & A_{1,2} & A_{1,3} & \dots & A_{1,n} \\ A_{2,1} & A_{2,2} & A_{2,3} & \dots & A_{2,n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ A_{m,1} & A_{m,2} & A_{m,3} & \dots & A_{m,n} \end{bmatrix}$

Where the numbers $A_{ij}$ are called the elements of the matrix. We describe matrices as wide if $n > m$ and tall if $n < m$. They are square iff $n = m$.

NOTE: naming convention for scalars vs. vectors vs. matrices.

Scalar Multiplication

Scalar multiplication of a matrix $\textit{A}$ and a scalar α is defined to be a new matrix $\textit{B}$, written $\textit{B} = \alpha\ \textit{A}$ or $\textit{B} = \textit{A} \alpha$, whose components are given by $b_{ij} = \alpha a_{ij}$.

Matrix Addition

Addition of two $m \times n$ -dimensional matrices $\textit{A}$ and $\textit{B}$ is defined as a new matrix $\textit{C}$, written $\textit{C} = \textit{A} + \textit{B}$, whose components $c_{ij}$ are given by addition of each component of the two matrices, $c_{ij} = a_{ij}+b_{ij}$.

Matrix Equality

Two matrices are equal when they share the same dimensions and all elements are equal. I.e.: $a_{ij}=b_{ij}$ for all $i \in I$ and $j \in J$.

Properties of Matrices

For three matrices $\mathbf{A}$, $\mathbf{B}$, and $\mathbf{C}$ we have the following properties

1. Commutative Law of Addition: $\mathbf{A} + \mathbf{B} = \mathbf{B} + \mathbf{A}$

2. Associative Law of Addition: $(\mathbf{A} + \mathbf{B}) + \mathbf{C} = \mathbf{A} + (\mathbf{B} + \mathbf{C})$

3. Associative Law of Multiplication: $\mathbf{A}(\mathbf{B}\mathbf{C}) = (\mathbf{A}\mathbf{B})\mathbf{C}$

4. Distributive Law: $\mathbf{A}(\mathbf{B} + \mathbf{C}) = \mathbf{A}\mathbf{B} + \mathbf{A}\mathbf{C}$

5. Identity: There is the matrix equivalent of one. We define a matrix $\mathbf{I_n}$ of dimension $n \times n$ such that the elements of $\mathbf{I_n}$ are all zero, except the diagonal elements $i=j$; where $I_{i,i} = 1$

6. Zero: We define a matrix $\mathbf 0$ of $m \times n$ dimension as the matrix where all components $(\mathbf 0)_{i,j}$ are 0

Identity Matrix

$I_3 = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1\\ \end{bmatrix}$

Here we can write $\textit{I}\textit{B} = \textit{B}\textit{I} = \textit{B}$ or $\textit{I}\textit{I} = \textit{I}$

Again, it is important to reiterate that matrices are not in general commutative with respect to multiplication. That is to say that the left and right products of matrices are, in general different.

$AB \neq BA$

Matrix Transpose

The transpose of a matrix $\textit{A}$ is formed by interchanging the rows and columns of $\textit{A}$. That is

$a_{ij}^T = a_{ji}$

Example 1:

$\textit{A} = \begin{bmatrix} 1 & 2 \\ 0 & 1 \\ \end{bmatrix}$

$\textit{A}^{T} = ?$

Matrix Transpose

The transpose of a matrix $\textit{A}$ is formed by interchanging the rows and columns of $\textit{A}$. That is

$a_{ij}^T = a_{ji}$

Example 1:

$\textit{A} = \begin{bmatrix} 1 & 2 \\ 0 & 1 \\ \end{bmatrix}$

$\textit{A}^{T} = \begin{bmatrix} 1 & 0 \\ 2 & 1 \\ \end{bmatrix}$

Matrix Transpose

The transpose of a matrix $\textit{A}$ is formed by interchanging the rows and columns of $\textit{A}$. That is

$a_{ij}^T = a_{ji}$

Example 2:

$\textit{B} = \begin{bmatrix} 1 & 2 \\ 0 & -3 \\ 3 & 1 \\ \end{bmatrix}$

$\textit{B}^{T} = ?$

Matrix Transpose

The transpose of a matrix $\mathbf A$ is formed by interchanging the rows and columns of $\mathbf A$. That is

$(\mathbf A)^T_{ij} = A_{ji}$

Example 2:

$\mathbf B = \begin{bmatrix} 1 & 2 \\ 0 & -3 \\ 3 & 1 \\ \end{bmatrix}$

$\mathbf{B}^{T} = \begin{bmatrix} 1 & 0 & 3 \\ 2 & -3 & 1 \\ \end{bmatrix}$

BONUS:

Show that $(\mathbf{A}\mathbf{B})^{T} = \mathbf{B}^{T}\mathbf{A}^{T}$.

Hint: the $ij$th element on both sides is $\sum_{k}A_{jk}A_{ki}$

Matrix-Vector Multiplication

Two perspectives:

1. Linear combination of columns

2. Dot product of vector with rows of matrix

$\begin{bmatrix} 2 & -6 \\ -1 & 4\\ \end{bmatrix} \begin{bmatrix} 2 \\ -1 \\ \end{bmatrix} = ?$

Test both ways out.

Lab: Matrix-vector multiplication

We just defined two different procedures for computing the matrix-vector product. Let us write them in Python.

Suppose we defined vectors as lists, and a matrix as a list of vectors.

1. Write code to compute the matrix vector product assuming $\mathbf A$ is a list of rows
2. Write code to compute the matrix vector product assuming $\mathbf A$ is a list of columns

Matrix Multiplication

Multiplication of an $m \times n$ -dimensional matrices $\textit{A}$ and a $n \times k$ matrix $\textit{B}$ is defined as a new matrix $\textit{C}$, written $\textit{C} = \textit{A}\textit{B}$, whose elements $C_{ij}$ are

$$ C_{i,j} = \sum_{l=1}^n A_{i,l}B_{l,j} $$

This can be memorized as row by column multiplication, where the value of each cell in the result is achieved by multiplying each element in a given row $i$ of the left matrix with its corresponding element in the column $j$ of the right matrix and adding the result of each operation together. This sum is the value of the new the new component $c_{ij}$.

Note that the product of matrices and vectors is a special case, under the assumption that the vector is oriented correctly and is of correct dimension (same rules as a matrix). In this case, we simply treat the vector as a $n \times 1$ or $1 \times n$ matrix.

Also note that $\textit{B}\textit{A} \neq \textit{A}\textit{B}$ in general.

Example 1:

$\textit{C} = \textit{A}\textit{B} = \begin{bmatrix} 1 & 2 \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 2 & 0 \\ 1 & 4 \\ \end{bmatrix} = \begin{bmatrix} 4 & 8 \\ 1 & 4 \\ \end{bmatrix}$

Example 2:

$\begin{bmatrix} 1 & 2 \\ 0 & -3 \\ 3 & 1 \\ \end{bmatrix} \begin{bmatrix} 2 & 6 & -3 \\ 1 & 4 & 0 \\ \end{bmatrix} = ?$

Example 2:

$\begin{bmatrix} 1 & 2 \\ 0 & -3 \\ 3 & 1 \\ \end{bmatrix} \begin{bmatrix} 2 & 6 & -3 \\ 1 & 4 & 0 \\ \end{bmatrix} = \begin{bmatrix} 4 & 14 & -3\\ -3 & -12 & 0 \\ 7 & 22 & -9\\ \end{bmatrix}$

Example 3:

$\begin{bmatrix} 2 & 6 & -3 \\ 1 & 4 & 0 \\ \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 0 & -3 \\ 3 & 1 \\ \end{bmatrix} = ?$

Example 3:

$\begin{bmatrix} 2 & 6 & -3 \\ 1 & 4 & 0 \\ \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 0 & -3 \\ 3 & 1 \\ \end{bmatrix} = \begin{bmatrix} -7 & -17\\ 1 & -10 \\ \end{bmatrix}$

Example 4:

$\begin{bmatrix} 2 & -6 \\ -1 & 4\\ \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix} = ?$

Example 4:

$\begin{bmatrix} 2 & -6 \\ -1 & 4\\ \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix} = \begin{bmatrix} 2\\ -1\\ \end{bmatrix}$

QUIZ:

Can you take the product of $\begin{bmatrix} 2 & -6 \\ -1 & 4\\ \end{bmatrix}$ and $\begin{bmatrix} 12 & 46 \\ \end{bmatrix}$ ?

If question seems vague, list all possible ways to address this question.

Lab: Matrix-matrix multiplication

There are yet more ways to programmatically implement matrix multiplication

Let us focus on just the two which are direct extensions of the preview matrix-vector multiplication methods

Use your dense vector functions to perform vector matrix multiplication - both by columns and by rows

Lab: Sparse Matrix Algebra

Consider the extension of sparse vectors to sparse matrices.

Write (completely) new functions to compute sparse matrix-matrix products.