Hacking Math I

Spring 2020

Topic 7: Linear Independence

This topic:

1. Vector spaces
2. Linear Independence
3. Orthogonality
4. Gram-Schmidt

Reading:

• I2ALA Chapter 5 (Linear Independence)

I. Vector Spaces

Vector space I

A vector space is a set of vectors with three additional properties (that not all sets of vectors have).

1. Contains origin
2. Closed under addition (of members of set)
3. Closed under scalar multiplication (of a member in the set)

Vector space II

Start with a set of vectors

$$ S = \{\mathbf v_1, \mathbf v_2, ..., \mathbf v_n\} $$

Think of these as your building blocks

A vector space is a new set consisting of all possible linear combinations of vectors in $S$.

This is called the span of a set of vectors:

\begin{align} V &= Span(S) \\ &= \{\alpha_1 \mathbf v_1 + \alpha_2 \mathbf v_2 + ... + \alpha_n \mathbf v_n \text{ for all } \alpha_1,\alpha_2,...,\alpha_n \in \mathbf R\} \end{align}

"Basis"

If the vectors in $S$ are linearly independent, they form a basis for $V$.

The dimension of a vector space is the cardinality of (all) its bases.

Basically, this is the smallest possible set of building blocks for the vector space

Example

Start with a set containing a single vector

$$ S = \{\mathbf v_1\} $$

What are the possible linear combinations of vectors in $Span(S)$?

\begin{align} V &= Span(S) \\ &= \{\alpha_1 \mathbf v_1 \text{ for all } \alpha_1 \in \mathbf R\} \end{align}

Example

Start with a set containing two vectors

$$ S = \{\mathbf v_1, \mathbf v_2\} $$

What are the possible linear combinations of vectors in $Span(S)$?

\begin{align} V &= Span(S) \\ &= \{\alpha_1 \mathbf v_1 + \alpha_2 \mathbf v_2 \text{ for all } \alpha_1, \alpha_2 \in \mathbf R\} \end{align}

II. Linear Independence

Slides courtesy of Boyd & Vandenberghe vmls-book.stanford.edu

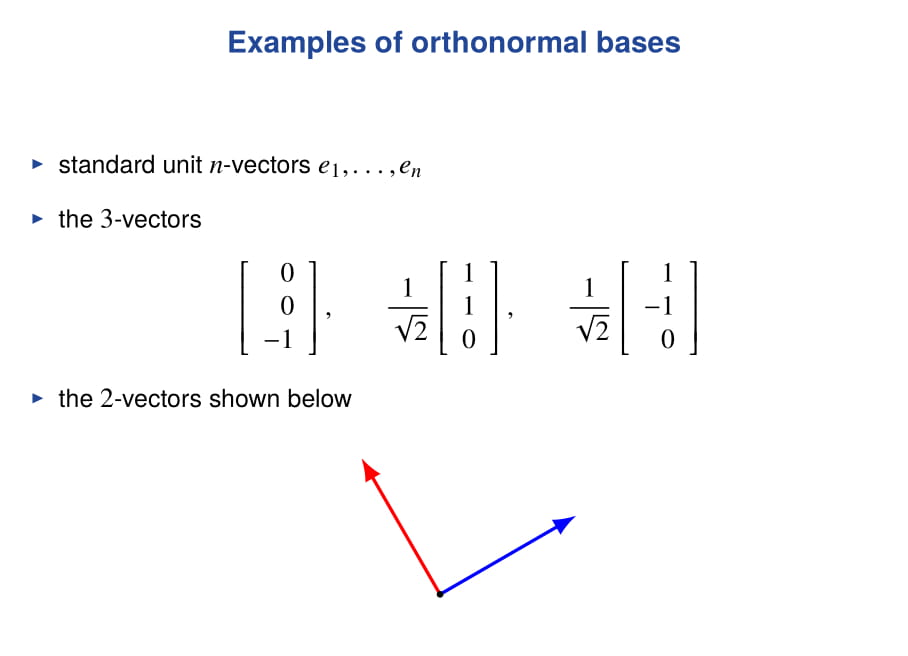
III. Orthogonality

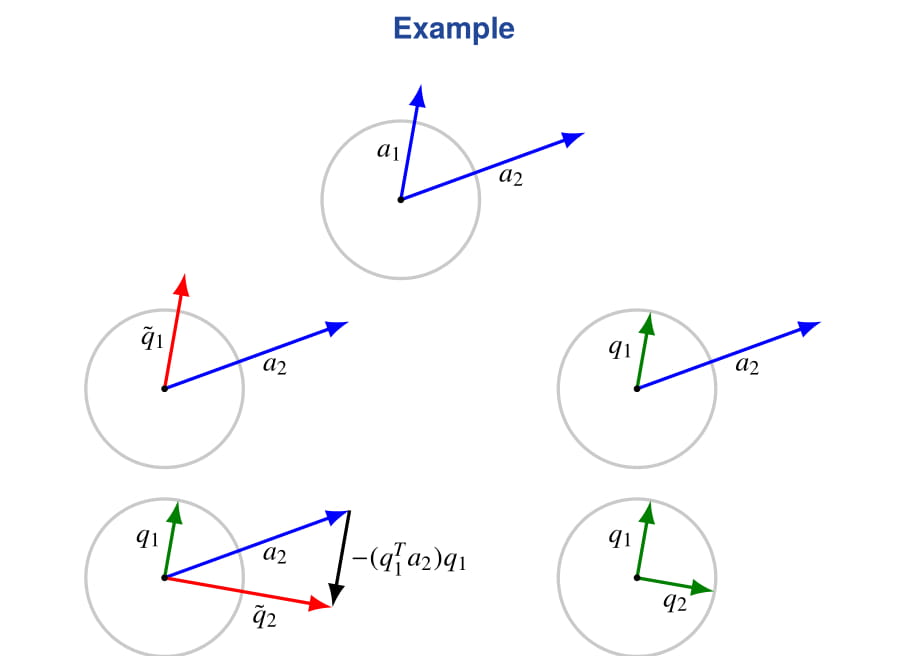
IV. Gram-Schmidt