Keith Dillon

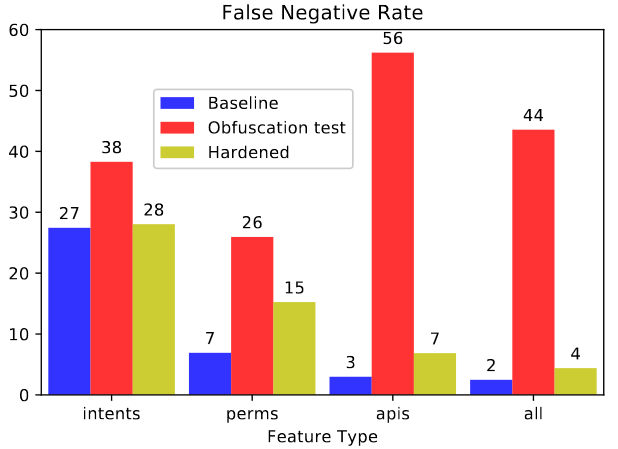
We consider the problem of detecting malware with deep learning models, where the malware may be combined with significant amounts of benign code. Examples of this include piggybacking and trojan horse attacks on a system, where malicious behavior is hidden within a useful application. Such added flexibility in augmenting the malware enables significantly more code obfuscation. Hence we focus on the use of static features, particularly Intents, Permissions, and API calls, which we presume cannot be ultimately hidden from the Android system, but only augmented with yet more such features. We first train a deep neural network classifier for malware classification using features of benign and malware samples. Then we demonstrate a steep increase in false negative rate (ie, attacks succeed), simply by randomly adding features of a benign app to malware. Finally we test the use of data augmentation to harden the classifier against such attacks. We find that for API calls, it is possible to reject the vast majority of attacks, where using Intents or Permissions is less successful.

https://arxiv.org/pdf/2002.05517

We derive an efficient method to perform clustering of nodes in Gaussian graphical models directly from sample data. Nodes are clustered based on the similarity of their network neighborhoods, with edge weights defined by partial correlations. In the limited-data scenario, where the covariance matrix would be rank-deficient, we are able to make use of matrix factors, and never need to estimate the actual covariance or precision matrix. We demonstrate the method on functional MRI data from the Human Connectome Project. A matlab implementation of the algorithm is provided.

https://arxiv.org/pdf/1910.02342

For Matlab code, read ‘more’

(more…)

While sparse inverse covariance matrices are very popular for modeling network connectivity, the value of the dense solution is often overlooked. In fact the L2-regularized solution has deep connections to a number of important applications to spectral graph theory, dimensionality reduction, and uncertainty quantification. We derive an approach to directly compute the partial correlations based on concepts from inverse problem theory. This approach also leads to new insights on open problems such as model selection and data preprocessing, as well as new approaches which relate the above application areas.

https://arxiv.org/pdf/1903.07181

We take an image science perspective on the problem of determining brain network connectivity given functional activity. But adapting the concept of image resolution to this problem, we provide a new perspective on network partitioning for individual brain parcellation. The typical goal here is to determine densely-interconnected subnetworks within a larger network by choosing the best edges to cut. We instead define these subnetworks as resolution cells, where highly-correlated activity within the cells makes edge weights difficult to determine from the data. Subdividing the resolution estimates into disjoint resolution cells via clustering yields a new variation, and new perspective, on spectral clustering. This provides insight and strategies for open questions such as the selection of model order and the optimal choice of preprocessing steps for functional imaging data. The approach is demonstrated using functional imaging data, where we find the proposed approach produces parcellations which are more predictive across multiple scans versus conventional methods, as well as versus alternative forms of spectral clustering.

https://arxiv.org/pdf/1810.04026