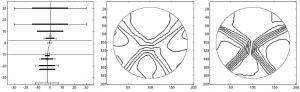
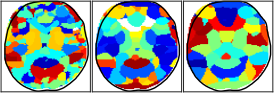
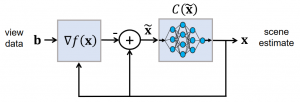
Model-based machine learning for computational reconstruction of opacity and missing information

Model-based machine learning methods incorporate domain knowledge from the physical forward model of an inverse problem to reduce the need for training data. In this research, we show how this can be used to address challenging limitations such as occlusion. We combine a convolutional neural network with a novel computational reconstruction method that combines source and attenuation distributions in order to model occlusion.

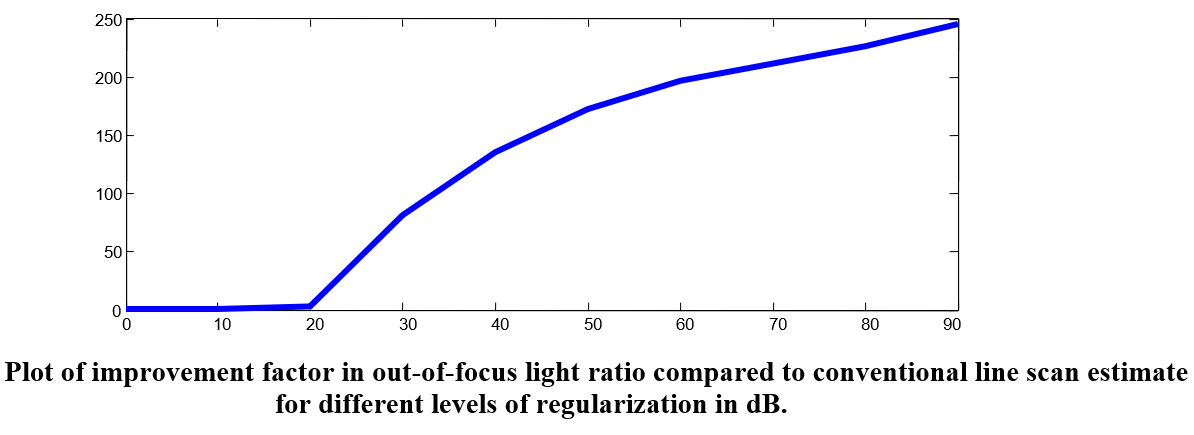
We demonstrate the ability to quickly learn to address reconstruction artifacts and opacity, forming a significantly improved final image of the scene based on as little as a single training image. The algorithm can be implemented efficiently and scaled to large problem sizes.

Link: Model-based machine learning for computational reconstruction of opacity and missing information

Optimization of freeform spectacle lenses based on high-order aberrations

Spectacle lenses are an important application of freeform manufacturing, with complex designs such as progressive lenses requiring nontraditional and specialized surface shapes. Such lenses also pose special challenges for optical design, as the eye’s gaze constantly changes relative to the lens. At the same time, many applications require sacrificing one region, such as the transition in a smooth bifocal, while achieving high quality in other regions. Common representations of freeform lens surfaces using polynomials or splines are poorly suited for such requirements. We describe an approach to optimize freeform spectacle lenses using a nonparametric representation of the surfaces at high resolution.

Requirements for smoothness are quantified in terms of high-order aberrations. This allows us to describe spatial variations in the design while also incorporating a constraint for optical smoothness and manufacturability. We show how this can be formulated as a regularized optimization problem incorporating raytracing, which can be solved efficiently. The approach can be used to design various kinds of lenses including progressive, bifocal, and lenticular designs. The designs have been successfully manufactured on multiple different brands of freeform generators. Manufactured lenses are found to perform as designed, including without polishing when supported by the material and generator.

Link: Optimization-of-freeform-spectacle-lenses-based-on-high-order-aberrations (pdf)

A first-order optimization method for learning to reconstruct opacity in computational imaging

Unknown self-occlusion in a scene with opaque objects causes the multiview reconstruction problem to become ill-posed and nonlinear. In this report we describe a scalable nonlinear optimization method for simultaneously reconstructing the object and occlusion. The approach uses a simple learning stage which forms hypotheses for scene opacity given locally-optimal reconstruction estimates. This is combined with a first-order projected-gradient method for imposing physical consistency. Results are demonstrated for simulated examples.

A first-order optimization method for learning to reconstruct opacity in computational imaging.pdf

S+SSPR 2020

I will be at S+SSPR 2020 (Statistical, Structural or Syntactic Pattern Recognition) on January 21-22 to present my research on partitioning of partial correlation networks.

 

Update 4/10/2021: Conference proceedings Dillon K. (2021) Efficient Partitioning of Partial Correlation Networks. In: Torsello A., Rossi L., Pelillo M., Biggio B., Robles-Kelly A. (eds) Structural, Syntactic, and Statistical Pattern Recognition. S+SSPR 2021. Lecture Notes in Computer Science, vol 12644. Springer, Cham. https://doi.org/10.1007/978-3-030-73973-7_17

 

Focus optimization in a Computational Confocal Microscope

In this report we consider the numerical optimization of performance for a computational extension of a confocal microscope. Using a system where the pinhole detector is replaced with a detector array, we seek to exploit this additional information for each point in the scan. We derive an optimal estimate of the light at focus which minimizes the contribution of out-of-focus light. We estimate the amount of improvement that would be theoretically possible in point-scanning and line-scanning systems and demonstrate with simulation. We find that even with a large degree of regularization, a significant improvement is possible, especially for line-scanning systems.

Focus optimization in a Computational Confocal Microscope

Robust neural network for wavefront reconstruction using Zernike coefficients

Accurately measuring optical aberrations is an important process for several eyecare tasks. Managing the individual variations found in human eyes plays a large role in properly defining these aberrations. A common method to measure optical aberrations uses sensors to locally capture the gradients across a grid of points. This data is used to reconstruct the wavefront resulting from light passing through the eye. In using this method of measurement, typical individual variations such as scarring or eyelashes can lead to shortcomings in the data. These shortcomings can manifest as noise or even areas of entirely missing data. The use of ANN (artificial neural networks) is one way to minimize the effects of these unpredictable deviations.

(more…)

The Resolution Matrix for Visualizing Functional Network Connectivity

The resolution matrix is a mathematical tool for analyzing inverse problems such as computational imaging systems. When treating network connectivity estimation as an inverse problem, the resolution matrix describes the degree to which network nodes and edges can be resolved. This is useful both for quantifying robustness of the network estimate, as well as identifying correlated activity. In this report we analyze the resolution matrix for functional MRI data from the Human Connectome project. We find that common metrics of the resolution metric can be used to identify networked activity, though with a new twist on the relationship between default mode network and the frontoparietal attention network.

https://arxiv.org/abs/2009.03187 (pdf).

Resolution-based spectral clustering for brain parcellation using functional MRI

Brain parcellation is important for exploiting neuroimaging data. Variability in physiology between individuals has led to the need for data-driven approaches to parcellation, with recent research focusing on simultaneously estimating and partitioning the network structure of the brain. We view data preprocessing, parcellation, and parcel validation from the perspective of predictive modeling. The goal is to identify parcels in a way that best generalizes to unseen data. We utilize an uncertainty quantification approach from image science to define parcels as groups of unresolvable variables in the predictive model.

(more…)